




Next: Vertical and horizontal resolution
Up: PHASE-SHIFT MIGRATION
Previous: Adjointness and ordinary differential
To examine questions of vertical exaggeration
and spatial resolution
we consider a line of point scatters along
a 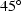 dipping line in (x,z)-space.
We impose a linear velocity gradient such as
that typically found in the Gulf of Mexico, i.e.
dipping line in (x,z)-space.
We impose a linear velocity gradient such as
that typically found in the Gulf of Mexico, i.e. 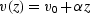 with
with 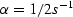 .Viewing our point scatterers as a function of traveltime depth,
.Viewing our point scatterers as a function of traveltime depth,
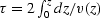 in Figure 11
we see, as expected,
that the points,
although separated by equal intervals in x,
are separated by shorter time intervals with increasing depth.
The points are uniformly separated
along a straight line in (x,z)-space,
but they are nonuniformly separated along a curved line
in
in Figure 11
we see, as expected,
that the points,
although separated by equal intervals in x,
are separated by shorter time intervals with increasing depth.
The points are uniformly separated
along a straight line in (x,z)-space,
but they are nonuniformly separated along a curved line
in 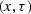 -space.
The curve is steeper near the earth's surface
where v(z) yields the greatest vertical exaggeration.
Here the vertical exaggeration is about unity (no exageration)
but deeper the vertical exaggeration is less than unity
(horizontal exaggeration).
-space.
The curve is steeper near the earth's surface
where v(z) yields the greatest vertical exaggeration.
Here the vertical exaggeration is about unity (no exageration)
but deeper the vertical exaggeration is less than unity
(horizontal exaggeration).
sagmod
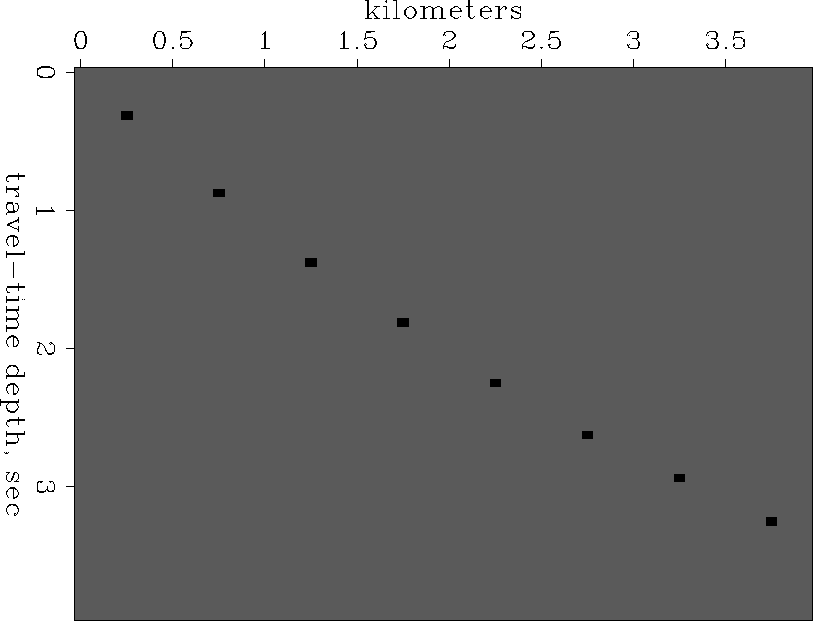
Figure 11
Points along a 45 degree slope as seen
as a function of traveltime depth.
|
|  |





Applying subroutine gazadj() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) the points spray out into hyperboloids (like hyperbolas, but not exactly)
shown in Figure 12.
The obvious feature of this synthetic data is that the hyperboloids
appear to have different asymptotes.
the points spray out into hyperboloids (like hyperbolas, but not exactly)
shown in Figure 12.
The obvious feature of this synthetic data is that the hyperboloids
appear to have different asymptotes.
sagdat
Figure 12
The points of Figure 11 diffracted
into hyperboloids.
|
|  |





In fact, there are no asymptotes because an asymptote
is a ray going horizontal at a more-or-less constant depth,
which will not happen in this model
because the velocity increases steadily with depth.
(I should get energetic and overlay these hyperboloids
on top of the exact hyperbolas of the Kirchhoff method,
to see if there are perceptible traveltime differences.)





Next: Vertical and horizontal resolution
Up: PHASE-SHIFT MIGRATION
Previous: Adjointness and ordinary differential
Stanford Exploration Project
12/26/2000


![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) the points spray out into hyperboloids (like hyperbolas, but not exactly)
shown in Figure 12.
The obvious feature of this synthetic data is that the hyperboloids
appear to have different asymptotes.
the points spray out into hyperboloids (like hyperbolas, but not exactly)
shown in Figure 12.
The obvious feature of this synthetic data is that the hyperboloids
appear to have different asymptotes.
