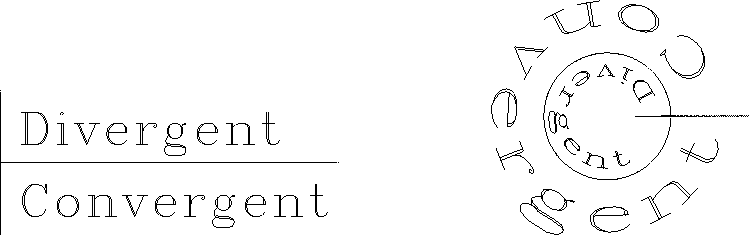Next: The meaning of divergence
Up: INSTABILITY
Previous: The unit circle
We are familiar with the fact that real values of  correspond to complex values of
correspond to complex values of 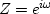 .Now let us look at complex values of
.Now let us look at complex values of  :
:
| 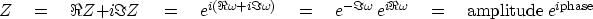 |
(44) |
Thus, when 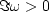 , |Z|<1.
In words, we transform the upper half of the
, |Z|<1.
In words, we transform the upper half of the  -plane
to the interior of the unit circle in the Z-plane.
Likewise, the stable region for poles is the lower half of the
-plane
to the interior of the unit circle in the Z-plane.
Likewise, the stable region for poles is the lower half of the
 -plane,
which is the exterior of the unit circle.
Figure 12 shows the transformation.
Some engineering books choose a different sign convention
(
-plane,
which is the exterior of the unit circle.
Figure 12 shows the transformation.
Some engineering books choose a different sign convention
(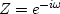 ),
but I selected the sign convention of physics.
Z
),
but I selected the sign convention of physics.
Z
Figure 12
Left is the complex  -plane
with axes
-plane
with axes 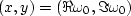 . Right is the Z-plane
with axes
. Right is the Z-plane
with axes 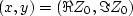 . The words ``Convergent'' and ``Divergent''
are transformed by
. The words ``Convergent'' and ``Divergent''
are transformed by 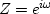 .
.










Next: The meaning of divergence
Up: INSTABILITY
Previous: The unit circle
Stanford Exploration Project
10/21/1998