




Next: Additivity of envelope entropy
Up: RELATED CONCEPTS
Previous: Prior and posterior distributions
Physicists
speak of maximizing entropy,
which, if we change the polarity, is like minimizing
the various Jensen inequalities.
As we minimize a Jensen inequality,
the small values tend to get larger
while the large values tend to get smaller.
For each population of values there is an average value,
i.e., a value that tends to get neither larger nor smaller.
The average depends not only on the population,
but also on the definition of entropy.
Commonly,
the pj are positive and 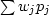 is an energy.
Typically the total energy, which will be fixed,
can be included as a constraint,
or we can find some other function to minimize.
For example,
divide both terms in (3) by the second term
and get an expression which is scale invariant;
i.e.,
scaling p leaves (15) unchanged:
is an energy.
Typically the total energy, which will be fixed,
can be included as a constraint,
or we can find some other function to minimize.
For example,
divide both terms in (3) by the second term
and get an expression which is scale invariant;
i.e.,
scaling p leaves (15) unchanged:
| 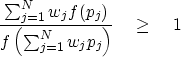 |
(15) |
Because the expression exceeds unity,
we are tempted to take a logarithm and make a new function
for minimization:
| ![\begin{displaymath}
J \eq \ln \left( \sum_j w_j f(p_j)\right)\ -\
\ln \left[ f \left( \sum_j w_j p_j\right)
\right] \quad \geq \quad 0\end{displaymath}](img26.gif) |
(16) |
Given a population pj of positive variants,
and an inequality like (16),
I am now prepared to define
the ``Jensen average'' 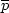 .Suppose there is one element,
say pJ,
of the population pj
that can be given a first-order perturbation,
and only a second-order perturbation in J will result.
Such an element is in
equilibrium and is the Jensen average
.Suppose there is one element,
say pJ,
of the population pj
that can be given a first-order perturbation,
and only a second-order perturbation in J will result.
Such an element is in
equilibrium and is the Jensen average 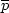 :
:
| ![\begin{displaymath}
0 \eq \left.
{\partial J\over\partial p_J}
\right] _{p_J = \overline{p}}\end{displaymath}](img28.gif) |
(17) |
Let fp denote the derivative of f with respect to its argument.
Inserting (16) into (17) gives
| 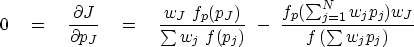 |
(18) |
Solving,
| 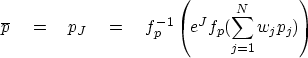 |
(19) |
But where do we get the function f,
and what do we say about the equilibrium value?
Maybe we can somehow derive f from the population.
If we cannot work out a general theory,
perhaps we can at least find the constant 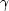 ,assuming the functional form to be
,assuming the functional form to be 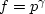 .
.





Next: Additivity of envelope entropy
Up: RELATED CONCEPTS
Previous: Prior and posterior distributions
Stanford Exploration Project
10/21/1998
![]() is an energy.
Typically the total energy, which will be fixed,
can be included as a constraint,
or we can find some other function to minimize.
For example,
divide both terms in (3) by the second term
and get an expression which is scale invariant;
i.e.,
scaling p leaves (15) unchanged:
is an energy.
Typically the total energy, which will be fixed,
can be included as a constraint,
or we can find some other function to minimize.
For example,
divide both terms in (3) by the second term
and get an expression which is scale invariant;
i.e.,
scaling p leaves (15) unchanged:
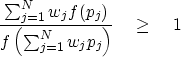
![\begin{displaymath}
J \eq \ln \left( \sum_j w_j f(p_j)\right)\ -\
\ln \left[ f \left( \sum_j w_j p_j\right)
\right] \quad \geq \quad 0\end{displaymath}](img26.gif)
![]() .Suppose there is one element,
say pJ,
of the population pj
that can be given a first-order perturbation,
and only a second-order perturbation in J will result.
Such an element is in
equilibrium and is the Jensen average
.Suppose there is one element,
say pJ,
of the population pj
that can be given a first-order perturbation,
and only a second-order perturbation in J will result.
Such an element is in
equilibrium and is the Jensen average ![]() :
:
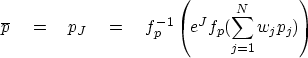
![]() ,assuming the functional form to be
,assuming the functional form to be ![]() .
.