# convolution: Y(Z) = X(Z) * B(Z)
#
subroutine convolve( nb, bb, nx, xx, yy )
integer nb # number of coefficients in filter
integer nx # number of coefficients in input
# number of coefficients in output will be nx+nb-1
real bb(nb) # filter coefficients
real xx(nx) # input trace
real yy(1) # output trace
integer ib, ix, iy, ny
ny = nx + nb -1
call null( yy, ny)
do ib= 1, nb
do ix= 1, nx
yy( ix+ib-1) = yy( ix+ib-1) + xx(ix) * bb(ib)
return; end
Some details of the Ratfor programming language are given in an appendix,
along with the subroutine 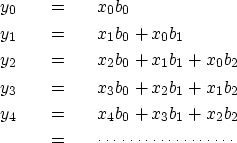
![\begin{displaymath}
\left[
\begin{array}
{c}
y_0 \
y_1 \
y_2 \
y_3...
...
\begin{array}
{c}
b_0 \
b_1 \
b_2 \end{array} \right]\end{displaymath}](img11.gif)
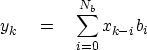
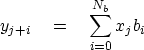
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , which erases the space for
the output.
, which erases the space for
the output.