




Next: (t,x,z)-Space, 15 degree Diffraction
Up: FINITE DIFFERENCING IN (t,
Previous: FINITE DIFFERENCING IN (t,
Migration and data synthesis may be envisioned
in ( z' , t' )-space
on the following table, which contains the upcoming wave U:
| 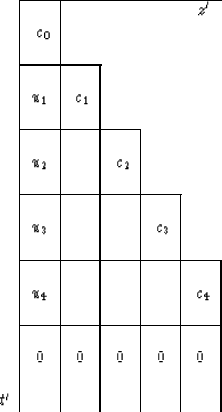 |
(48) |
In this table the observed upcoming wave
at the earth's surface z' = 0 is denoted by ut.
The migrated section, denoted by ct,
is depicted along the diagonal because the imaging
condition of exploding reflectors at
time t = 0 is represented in
retarded space as
| 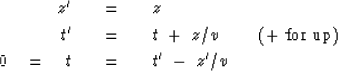 |
(49) |
| (50) |
| (51) |
The best-focused migration need not
fall on the 45 line as depicted in (48);
it might be on any line or curve as determined by
the earth velocity.
This curve forms the basis for velocity determination.
You couldn't determine velocity this way in the frequency-domain.
line as depicted in (48);
it might be on any line or curve as determined by
the earth velocity.
This curve forms the basis for velocity determination.
You couldn't determine velocity this way in the frequency-domain.
The equation for upcoming waves U in
retarded coordinates (t' , x' , z' ) is
| 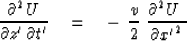 |
(52) |
Next, Fourier transform the x-axis.
This assumes that v is a constant function of x and
that the x-dependence of U is the
sinusoidal function 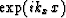 .Thus,
.Thus,
| 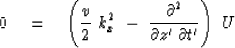 |
(53) |
Now this partial-differential equation will be discretized
with respect to t' and z'.
Matrix notation will be used, but the notation does not refer to matrix algebra.
Instead the matrices refer to differencing stars that may be placed
on the 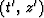 -plane of (48).
Let
-plane of (48).
Let  denote convolution in
denote convolution in 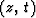 -space.
A succession of derivatives is really a convolution, so
the concept of
-space.
A succession of derivatives is really a convolution, so
the concept of 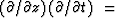
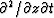 is expressed by
is expressed by
| ![\begin{displaymath}[ \ -1 \ \ \ +1 \ ]
\ \ \ { {\rm *} } \ \ \
\left[
\matrix {...
...eft[
\begin{array}
{rr}
1 & -1 \\ -1 & 1 \\ \end{array}\right]\end{displaymath}](img111.gif) |
(54) |
Thus, the differenced form of (53) is
| ![\begin{displaymath}
0 \eq \left\{
{v \over 2 }\ { \Delta z' \, \Delta t' \over 4...
... & -1 \\ -1 & 1 \\ \end{array}\right]
\ \right\}
\ {{\rm *}}\ U\end{displaymath}](img112.gif) |
(55) |
The 1/4 enters in because the average of U
is taken over four places on the mesh.
The sum of the two operators always has 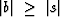 in the form
in the form
| ![\begin{displaymath}
0 \eq \ \ \left[ \matrix {
\matrix { \ s \cr \ b }
\matrix { b\ \cr s\ }
} \right]
\ \ \ {{\rm *}}\ \ U\end{displaymath}](img114.gif) |
(56) |
Now the differencing star in (56) will be used to fill the
table (48) with values for U.
Given the three values of U in the boxes, a missing one, M, may be
determined by either of the implied two operations
|  |
(57) |
It turns out that because 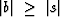 , the
implied filling operations by
, the
implied filling operations by
|  |
(58) |
are unstable.
It is obvious that there would be a
zero-divide problem if s were equal to 0,
and it is not difficult to do the stability analysis
that shows that (58)
causes exponential growth of small disturbances.
It is a worthwhile
exercise to make the zero-dip assumption ( kx = 0 ) and use
the numerical values in the operator of (56) to fill in the elements
of the table (48).
It will be found that the values of ut move
laterally in z across the table with no change,
predicting, as the table should, that ct = ut.
Slow change in z suggests that we
have oversampled the z-axis.
In practice, effort is saved by sampling the z-axis
with fewer points than are used to sample the t-axis.





Next: (t,x,z)-Space, 15 degree Diffraction
Up: FINITE DIFFERENCING IN (t,
Previous: FINITE DIFFERENCING IN (t,
Stanford Exploration Project
10/31/1997


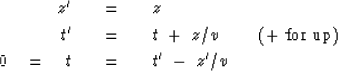
![]() line as depicted in (48);
it might be on any line or curve as determined by
the earth velocity.
This curve forms the basis for velocity determination.
You couldn't determine velocity this way in the frequency-domain.
line as depicted in (48);
it might be on any line or curve as determined by
the earth velocity.
This curve forms the basis for velocity determination.
You couldn't determine velocity this way in the frequency-domain.
![]() -plane of (48).
Let
-plane of (48).
Let ![]() denote convolution in
denote convolution in ![]() -space.
A succession of derivatives is really a convolution, so
the concept of
-space.
A succession of derivatives is really a convolution, so
the concept of ![]()
![]() is expressed by
is expressed by
![]() in the form
in the form

