At the heart of the migration process is the operation
of downward continuing data.
Given the input data on the plane of the earth's surface z=0,
we must manufacture the data that could be recorded at depth z.
This is most easily done in the Fourier domain.
Mathematically shifting on the z-axis is like
shifting on the time t-axis.
To shift on time by an amount t0 we multiply by ![]() and
to shift on depth by an amount z0 we multiply by
and
to shift on depth by an amount z0 we multiply by ![]() .It is not quite this trivial however:
the data field is not evidently a function of kz because
we do not have data given on a z-axis so we cannot
simply Fourier transform it to kz.
Instead we have
.It is not quite this trivial however:
the data field is not evidently a function of kz because
we do not have data given on a z-axis so we cannot
simply Fourier transform it to kz.
Instead we have
| |
(9) |
 |
Downward continuation is a product relationship
in both the ![]() -domain and the kx-domain.
What does the filter look like in the time and space domain?
It turns out like a cone, that is,
it is roughly an impulse function
of
-domain and the kx-domain.
What does the filter look like in the time and space domain?
It turns out like a cone, that is,
it is roughly an impulse function
of ![]() .More precisely, it is the Huygens secondary wave source
that was exemplified by ocean waves entering a gap through a storm barrier.
Adding up the response of multiple gaps in
the barrier would be convolution over x.
Superposing many incident ocean waves would be convolution over t.
.More precisely, it is the Huygens secondary wave source
that was exemplified by ocean waves entering a gap through a storm barrier.
Adding up the response of multiple gaps in
the barrier would be convolution over x.
Superposing many incident ocean waves would be convolution over t.
Now let us see why the downward continuation filter
has the mathematical form stated.
Every point in the ![]() -plane refers to a sinusoidal plane wave.
The variation with depth will also be sinusoidal,
namely
-plane refers to a sinusoidal plane wave.
The variation with depth will also be sinusoidal,
namely ![]() .The value of kz for the plane wave
is found simply by solving equation (8):
.The value of kz for the plane wave
is found simply by solving equation (8):
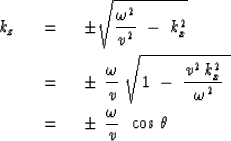 |
(10) | |
| (11) | ||
| (12) |
Mathematically we can imagine an arbitrary function of t, x, and z.
Its three-dimensional Fourier transform fills a volume in the space of
![]() , kx, and kz.
This arbitrary function is not a wavefield unless it vanishes
everywhere except the cone-shaped surface
, kx, and kz.
This arbitrary function is not a wavefield unless it vanishes
everywhere except the cone-shaped surface
![]() given by the wave equation.
Thus equation (9) makes sense even though we
cannot Fourier transform data over the z-axis because we
don't observe data along the z-axis.
It makes sense because if we know the mathematical function
is a wavefield and if we know its Fourier transform over
given by the wave equation.
Thus equation (9) makes sense even though we
cannot Fourier transform data over the z-axis because we
don't observe data along the z-axis.
It makes sense because if we know the mathematical function
is a wavefield and if we know its Fourier transform over
![]() and kx, then we know its Fourier transform at any kz
and we can ``delay'' it in z (downward shift)
by multiplying by
and kx, then we know its Fourier transform at any kz
and we can ``delay'' it in z (downward shift)
by multiplying by ![]() .
.
The input-output filter, being of the form ![]() , appears
to be a phase-shifting filter with
no amplitude scaling.
This bodes well for our plans to deconvolve.
It means that signal-to-noise power considerations will be much
less relevant for migration than for ordinary filtering.
, appears
to be a phase-shifting filter with
no amplitude scaling.
This bodes well for our plans to deconvolve.
It means that signal-to-noise power considerations will be much
less relevant for migration than for ordinary filtering.
| (13) |
| (14) |