




Next: NULL SPACE AND INTERVAL
Up: Preconditioning
Previous: The preconditioned solver
Recall the fitting goals (10)
| 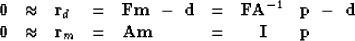 |
(10) |
Without preconditioning we have the search direction
| ![\begin{displaymath}
\Delta \bold m_{\rm bad} \quad =\quad
\left[
\begin{array}
...
... \begin{array}
{c}
\bold r_d \\ \bold r_m
\end{array}\right]\end{displaymath}](img40.gif) |
(11) |
and with preconditioning we have the search direction
| ![\begin{displaymath}
\Delta \bold p_{\rm good} \quad =\quad
\left[
\begin{array}...
... \begin{array}
{c}
\bold r_d \\ \bold r_m
\end{array}\right]\end{displaymath}](img41.gif) |
(12) |
The essential feature of preconditioning is not that we perform
the iterative optimization in terms of the variable 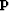 .The essential feature is that we use a search direction
that is a gradient with respect to
.The essential feature is that we use a search direction
that is a gradient with respect to 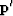 not
not 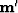 .Using
.Using 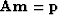 we have
we have
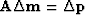 .This enables us to define a good search direction in model space.
.This enables us to define a good search direction in model space.
| 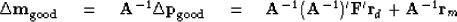 |
(13) |
Define the gradient by 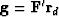 and
notice that
and
notice that 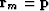 .
.
| 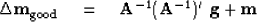 |
(14) |
The search direction (14)
shows a positive-definite operator scaling the gradient.
Each component of any gradient vector is independent of each other.
All independently point a direction for descent.
Obviously, each can be scaled by any positive number.
Now we have found that we can also scale a gradient vector by
a positive definite matrix and we can still expect
the conjugate-direction algorithm to descend, as always,
to the ``exact'' answer in a finite number of steps.
This is because modifying the search direction with
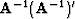 is equivalent to solving
a conjugate-gradient problem in
is equivalent to solving
a conjugate-gradient problem in 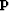 .
.





Next: NULL SPACE AND INTERVAL
Up: Preconditioning
Previous: The preconditioned solver
Stanford Exploration Project
4/27/2004
![]() .The essential feature is that we use a search direction
that is a gradient with respect to
.The essential feature is that we use a search direction
that is a gradient with respect to ![]() not
not ![]() .Using
.Using ![]() we have
we have
![]() .This enables us to define a good search direction in model space.
.This enables us to define a good search direction in model space.
![]() is equivalent to solving
a conjugate-gradient problem in
is equivalent to solving
a conjugate-gradient problem in ![]() .
.