![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows two waves of opposite polarity crossing each other.
shows two waves of opposite polarity crossing each other.
Theoretically, a scale-factor problem arises
because locally, wavefields, not energies, add.
Nodes on standing waves are familiar from theory,
but they could give you the wrong idea that the concept of node
is one that applies only with sinusoids.
Actually, destructive interference arises
anytime a polarity-reversed waveform bounces back and crosses itself.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows two waves of opposite polarity crossing each other.
shows two waves of opposite polarity crossing each other.
|
super90
Figure 3 Superposition of plane waves of opposite polarity. | 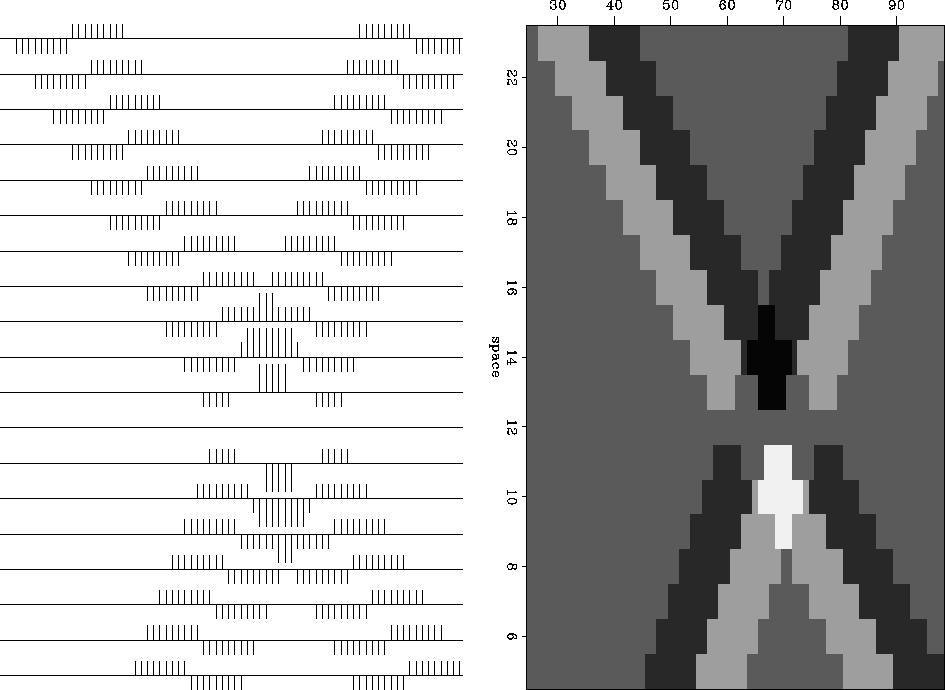 |
Observe that one seismogram has a zero-valued signal,
while its neighbors have anomalously higher amplitudes
and higher energies than are found far away from the interference.
The situation shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) does not occur easily in nature.
Reflection naturally comes to mind,
but usually the reflected wave
crosses the incident wave at a later time and then they don't extinguish.
Approximate extinguishing occurs rather easily
when waves are quasi-monochromatic.
We will soon see, however,
that methodologies for finding scales all begin with deconvolution
and that eliminates the monochromatic waves.
does not occur easily in nature.
Reflection naturally comes to mind,
but usually the reflected wave
crosses the incident wave at a later time and then they don't extinguish.
Approximate extinguishing occurs rather easily
when waves are quasi-monochromatic.
We will soon see, however,
that methodologies for finding scales all begin with deconvolution
and that eliminates the monochromatic waves.