




Next: About this document ...
Up: Empty bins and inverse
Previous: Abandoned theory for matching
First we first look at data 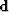 .Then we think about a model
.Then we think about a model 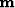 ,and an operator
,and an operator 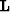 to link the model and the data.
Sometimes the operator is merely the first term in a series expansion
about
to link the model and the data.
Sometimes the operator is merely the first term in a series expansion
about 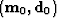 .Then we fit
.Then we fit
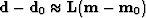 .To fit the model, we must reduce the fitting residuals.
Realizing that the importance of a data residual
is not always simply the size of the residual
but is generally a function of it,
we conjure up (topic for later chapters)
a weighting function (which could be a filter) operator
.To fit the model, we must reduce the fitting residuals.
Realizing that the importance of a data residual
is not always simply the size of the residual
but is generally a function of it,
we conjure up (topic for later chapters)
a weighting function (which could be a filter) operator 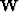 .This defines our data residual:
.This defines our data residual:
| ![\begin{displaymath}
\bold r_d \eq \bold W
[ \bold L
( \bold m-\bold m_0)
\ -\
( \bold d-\bold d_0)
]\end{displaymath}](img91.gif) |
(19) |
Next we realize that the data might not be adequate to determine the model,
perhaps because our comfortable dense sampling of the model
ill fits our economical sparse sampling of data.
Thus we adopt a fitting goal that mathematicians call ``regularization''
and we might call a ``model style'' goal
or more simply,
a quantification of our prejudice about models.
We express this by choosing an operator 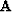 ,often simply a roughener like a gradient
(the choice again a topic in this and later chapters).
It defines our model residual by
,often simply a roughener like a gradient
(the choice again a topic in this and later chapters).
It defines our model residual by
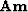 or
or
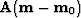 , say we choose
, say we choose
| 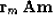 |
(20) |
In an ideal world, our model prejudice would not conflict
with measured data, however,
life is not so simple.
Since conflicts between data and preconceived notions invariably arise
(and they are why we go to the expense of acquiring data)
we need an adjustable parameter
that measures our ``bullheadedness'', how much we intend
to stick to our preconceived notions in spite of contradicting data.
This parameter is generally called epsilon  because we like to imagine that our bullheadedness is small.
(In mathematics,
because we like to imagine that our bullheadedness is small.
(In mathematics,  is often taken to be
an infinitesimally small quantity.)
Although any bullheadedness seems like a bad thing,
it must be admitted that measurements are imperfect too.
Thus as a practical matter we often find ourselves minimizing
is often taken to be
an infinitesimally small quantity.)
Although any bullheadedness seems like a bad thing,
it must be admitted that measurements are imperfect too.
Thus as a practical matter we often find ourselves minimizing
| 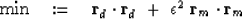 |
(21) |
and wondering what to choose for  .I have two suggestions:
My simplest suggestion is to choose
.I have two suggestions:
My simplest suggestion is to choose  so that the residual of data fitting matches that of model styling.
Thus
so that the residual of data fitting matches that of model styling.
Thus
| 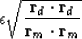 |
(22) |
My second suggestion is to think of the force on our final solution.
In physics, force is associated with a gradient.
We have a gradient for the data fitting
and another for the model styling:
| 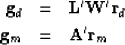 |
(23) |
| (24) |
We could balance these forces by the choice
| 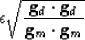 |
(25) |
Although we often ignore  in discussing the formulation
of a problem, when time comes to solve the problem, reality intercedes.
Generally,
in discussing the formulation
of a problem, when time comes to solve the problem, reality intercedes.
Generally, 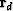 has different physical units than
has different physical units than 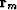 (likewise
(likewise 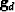 and
and 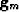 )and we cannot allow our solution
to depend on the accidental choice of units
in which we express the problem.
I have had much experience choosing
)and we cannot allow our solution
to depend on the accidental choice of units
in which we express the problem.
I have had much experience choosing  , but it is
only recently that I boiled it down to the above two suggestions.
Normally I also try other values, like double or half those
of the above choices,
and I examine the solutions for subjective appearance.
If you find any insightful examples, please tell me about them.
, but it is
only recently that I boiled it down to the above two suggestions.
Normally I also try other values, like double or half those
of the above choices,
and I examine the solutions for subjective appearance.
If you find any insightful examples, please tell me about them.
Computationally, we could choose a new  with each iteration,
but it is more expeditious
to freeze
with each iteration,
but it is more expeditious
to freeze  , solve the problem,
recompute
, solve the problem,
recompute  , and solve the problem again.
I have never seen a case where more than one iteration was necessary.
, and solve the problem again.
I have never seen a case where more than one iteration was necessary.
People who work with small problems
(less than about 103 vector components)
have access to an attractive theoretical approach
called cross-validation.
Simply speaking,
we could solve the problem many times,
each time omitting a different data value.
Each solution would provide a model
that could be used to predict
the omitted data value.
The quality of these predictions
is a function of  and this provides a guide to finding it.
My objections to cross validation are two-fold:
First, I don't know how to apply it in the large problems
like we solve in this book
(I should think more about it);
and second,
people who worry much about
and this provides a guide to finding it.
My objections to cross validation are two-fold:
First, I don't know how to apply it in the large problems
like we solve in this book
(I should think more about it);
and second,
people who worry much about  ,perhaps first should think
more carefully about
their choice of the filters
,perhaps first should think
more carefully about
their choice of the filters 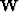 and
and 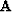 ,which is the focus of this book.
Notice that both
,which is the focus of this book.
Notice that both 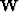 and
and 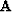 can be defined with a scaling factor which is like scaling
can be defined with a scaling factor which is like scaling  .Often more important in practice,
with
.Often more important in practice,
with 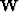 and
and 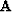 we have a scaling factor that need not be constant but
can be a function of space or spatial frequency
within the data space and/or model space.
we have a scaling factor that need not be constant but
can be a function of space or spatial frequency
within the data space and/or model space.





Next: About this document ...
Up: Empty bins and inverse
Previous: Abandoned theory for matching
Stanford Exploration Project
4/27/2004
![]() ,often simply a roughener like a gradient
(the choice again a topic in this and later chapters).
It defines our model residual by
,often simply a roughener like a gradient
(the choice again a topic in this and later chapters).
It defines our model residual by
![]() or
or
![]() , say we choose
, say we choose
![]() because we like to imagine that our bullheadedness is small.
(In mathematics,
because we like to imagine that our bullheadedness is small.
(In mathematics, ![]() is often taken to be
an infinitesimally small quantity.)
Although any bullheadedness seems like a bad thing,
it must be admitted that measurements are imperfect too.
Thus as a practical matter we often find ourselves minimizing
is often taken to be
an infinitesimally small quantity.)
Although any bullheadedness seems like a bad thing,
it must be admitted that measurements are imperfect too.
Thus as a practical matter we often find ourselves minimizing
![]() with each iteration,
but it is more expeditious
to freeze
with each iteration,
but it is more expeditious
to freeze ![]() , solve the problem,
recompute
, solve the problem,
recompute ![]() , and solve the problem again.
I have never seen a case where more than one iteration was necessary.
, and solve the problem again.
I have never seen a case where more than one iteration was necessary.
![]() and this provides a guide to finding it.
My objections to cross validation are two-fold:
First, I don't know how to apply it in the large problems
like we solve in this book
(I should think more about it);
and second,
people who worry much about
and this provides a guide to finding it.
My objections to cross validation are two-fold:
First, I don't know how to apply it in the large problems
like we solve in this book
(I should think more about it);
and second,
people who worry much about ![]() ,perhaps first should think
more carefully about
their choice of the filters
,perhaps first should think
more carefully about
their choice of the filters ![]() and
and ![]() ,which is the focus of this book.
Notice that both
,which is the focus of this book.
Notice that both ![]() and
and ![]() can be defined with a scaling factor which is like scaling
can be defined with a scaling factor which is like scaling ![]() .Often more important in practice,
with
.Often more important in practice,
with ![]() and
and ![]() we have a scaling factor that need not be constant but
can be a function of space or spatial frequency
within the data space and/or model space.
we have a scaling factor that need not be constant but
can be a function of space or spatial frequency
within the data space and/or model space.