if adjoint
then erase x
if operator itself
then erase y
do iy = 1, ny {
do ix = 1, nx {
if adjoint
x(ix) = x(ix) + b(iy,ix) 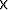 y(iy)
if operator itself
y(iy) = y(iy) + b(iy,ix)
y(iy)
if operator itself
y(iy) = y(iy) + b(iy,ix) 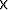 x(ix)
}}
x(ix)
}}
Notice that the ``bottom line'' in the program is that x and y are simply interchanged. The above example is a prototype of many to follow, so observe carefully the similarities and differences between the adjoint and the operator itself.
Next we restate the matrix-multiply pseudo code in real code,
in a language called Loptran![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) ,
a language designed for
exposition and research
in model fitting and optimization in physical sciences.
The module matmult
for matrix multiply and its adjoint
exhibits the style that we will use repeatedly.
At last count there were 53 such routines
(operator with adjoint)
in this book alone.
matmultmatrix multiply
Notice that the module matmult
does not explicitly erase its output before it begins,
as does the psuedo code.
That is because Loptran will always erase for you
the space required for the operator's output.
Loptran also defines a logical variable adj
for you to distinguish your computation of the adjoint
x=x+B'*y
from the forward operation
y=y+B*x.
In computerese, the two lines beginning #% are macro expansions
that take compact bits of information which expand
into the verbose boilerplate that Fortran requires.
Loptran is Fortran with these macro expansions.
You can always see how they expand by looking at
http://sep.stanford.edu/sep/prof/gee/Lib/.
,
a language designed for
exposition and research
in model fitting and optimization in physical sciences.
The module matmult
for matrix multiply and its adjoint
exhibits the style that we will use repeatedly.
At last count there were 53 such routines
(operator with adjoint)
in this book alone.
matmultmatrix multiply
Notice that the module matmult
does not explicitly erase its output before it begins,
as does the psuedo code.
That is because Loptran will always erase for you
the space required for the operator's output.
Loptran also defines a logical variable adj
for you to distinguish your computation of the adjoint
x=x+B'*y
from the forward operation
y=y+B*x.
In computerese, the two lines beginning #% are macro expansions
that take compact bits of information which expand
into the verbose boilerplate that Fortran requires.
Loptran is Fortran with these macro expansions.
You can always see how they expand by looking at
http://sep.stanford.edu/sep/prof/gee/Lib/.
What is new in Fortran 90, and will be a big help to us,
is that instead of a subroutine with a single entry,
we now have a module with two entries,
one named _init
for the physical scientist who defines the physical problem by
defining the matrix, and
another named _lop
for the least-squares problem solver,
the computer scientist who will not be interested
in how we specify ![]() , but who will be iteratively computing
, but who will be iteratively computing
![]() and
and ![]() to optimize the model fitting.
The lines beginning with #% are expanded by Loptran into
more verbose and distracting Fortran 90 code.
The second line in the module matmult,
however,
is pure Fortran syntax saying that
bb is a pointer to a real-valued matrix.
to optimize the model fitting.
The lines beginning with #% are expanded by Loptran into
more verbose and distracting Fortran 90 code.
The second line in the module matmult,
however,
is pure Fortran syntax saying that
bb is a pointer to a real-valued matrix.
To use matmult, two calls must be made, the first one
call matmult_init( bb)
is done by the physical scientist after he or she has prepared the matrix.
Most later calls will be done by numerical analysts
in solving code like in Chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
These calls look like
.
These calls look like
stat = matmult_lop( adj, add, x, y)
where adj is the logical variable saying whether we desire
the adjoint or the operator itself,
and where add is a logical variable saying
whether we want to accumulate like
Operator initialization often allocates memory. To release this memory, you can call matmult_close() although in this case nothing really happens.
We split operators into two independent processes, the first is used for geophysical set up while the second is invoked by mathematical library code (introduced in the next chapter) to find the model that best fits the data. Here is why we do so. It is important that the math code contain nothing about the geophysical particulars. This enables us to use the same math code on many different geophysical problems. This concept of ``information hiding'' arrived late in human understanding of what is desireable in a computer language. This feature alone is valuable enough to warrant upgrading from Fortran 77 to Fortran 90, and likewise from C to C++. Subroutines and functions are the way that new programs use old ones. Object modules are the way that old programs (math solvers) are able to use new ones (geophysical operators).