|
3-2
Figure 2 Percent of total energy in a filter between time and time t. | 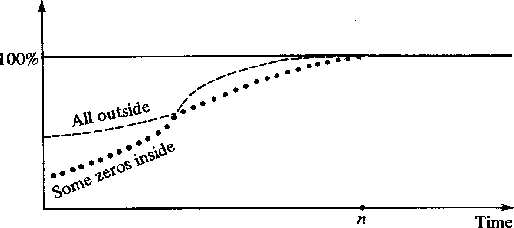 |
|
3-2
Figure 2 Percent of total energy in a filter between time and time t. |  |
We will compare two wavelets ![]() and
and ![]() which are
identical except for one zero,
which is outside the unit circled for
which are
identical except for one zero,
which is outside the unit circled for
![]() and inside for
and inside for ![]() .We may write this as
.We may write this as
| t | ||||
| bp0 | sp0 | |||
| 1 | bp1 + sp0 | sp1 + bp0 | ||
| k | bpk + spk -1 | spk + bpk -1 | ||
| n + 1 | spn | bpn | (b2 - s2) (-pn2) |
The difference, which is given in the right-hand column, is clearly always positive.
To prove that the minimum-phase wavelet delays energy the least, the preceding argument is repeated with each of the roots until they are all outside the unit circle.