




Next: Time domain
Up: END OF CHAPTER FOR
Previous: Lateral velocity variation again
The customary numerical solution to the x-domain forms of the equations
in Tables ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .4 and
.4 and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .5 is arrived at by splitting.
That is, you march forward a small
.5 is arrived at by splitting.
That is, you march forward a small 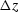 -step alternately
with the two extrapolators
-step alternately
with the two extrapolators
|  |
(71) |
| (72) |
The first equation, called the
lens equation,
is solved analytically:
| 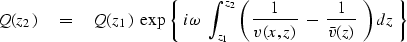 |
(73) |
Migration that includes the lens equation
is called depth migration.
Migration that omits this term is called
time migration.
Observe that the diffraction parts
of Tables ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .4 and
.4 and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .5 are the same.
Let us use them and equation (
.5 are the same.
Let us use them and equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) to
define a table of diffraction equations.
Substitute
) to
define a table of diffraction equations.
Substitute 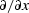 for i kx and
clear
for i kx and
clear 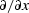 from the denominators to
get Table
from the denominators to
get Table ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .6.
.6.
Table:
Diffraction equations for laterally variable media.
| |
|
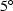 |
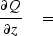 zero zero |
| |
|
| |
|
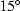 |
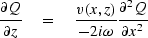 |
| |
|
| |
|
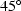 |
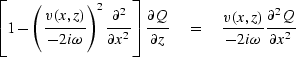 |
| |
|
You may wonder where the two velocities v(x,z) and 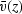 came from.
The first arises in the wave equation,
and it must be x-variable if the model is x-variable.
The second arises in a mathematical transformation,
namely, equation (
came from.
The first arises in the wave equation,
and it must be x-variable if the model is x-variable.
The second arises in a mathematical transformation,
namely, equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ),
so it is purely a matter of definition.
),
so it is purely a matter of definition.





Next: Time domain
Up: END OF CHAPTER FOR
Previous: Lateral velocity variation again
Stanford Exploration Project
12/26/2000

![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .4 and
.4 and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .5 is arrived at by splitting.
That is, you march forward a small
.5 is arrived at by splitting.
That is, you march forward a small 
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .4 and
.4 and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .5 are the same.
Let us use them and equation (
.5 are the same.
Let us use them and equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) to
define a table of diffraction equations.
Substitute
) to
define a table of diffraction equations.
Substitute ![]() for i kx and
clear
for i kx and
clear ![]() from the denominators to
get Table
from the denominators to
get Table ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .6.
.6.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ),
so it is purely a matter of definition.
),
so it is purely a matter of definition.