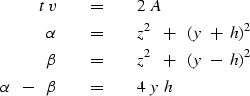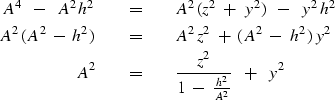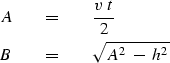Next: INTRODUCTION TO DIP
Up: PRESTACK MIGRATION
Previous: Prestack migration ellipse
Considering h in equation (6)
to be a constant,
enables us to write a subroutine for migrating constant-offset sections.
Subroutine flathyp() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) is easily prepared
from subroutine kirchfast()
is easily prepared
from subroutine kirchfast() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) by
replacing its hyperbola equation with equation (6).
by
replacing its hyperbola equation with equation (6).
# Flat topped hyperbolas and constant-offset section migration
#
subroutine flathyp( adj, add, vel , h, t0,dt,dx, modl,nt,nx, data)
integer ix,iz,it,ib, adj, add, nt,nx
real t, amp, z,b, vel(nt), h, t0,dt,dx, modl(nt,nx),data(nt,nx)
call adjnull( adj, add, modl,nt*nx, data,nt*nx)
do ib= -nx, nx { b = dx * ib # b = midpt separation y-y0
do iz= 2, nt { z = t0 + dt * (iz-1) # z = zero-offset time
t = .5 * ( sqrt( z**2 +((b-h)*2/vel(iz))**2) +
sqrt( z**2 +((b+h)*2/vel(iz))**2) )
it = 1.5 + (t - t0) / dt
if( it > nt ) break
amp = (z/t)/ sqrt(t)
do ix= max0(1, 1-ib), min0(nx, nx-ib)
if( adj == 0 )
data(it,ix+ib)= data(it,ix+ib) + modl(iz,ix ) * amp
else
modl(iz,ix )= modl(iz,ix ) + data(it,ix+ib) * amp
}
}
return; end
The amplitude in subroutine flathyp()
should be improved when we have time to do so.
Forward and backward responses to impulses
of subroutine flathyp()
are found in Figures 4 and 5.
Cos.1
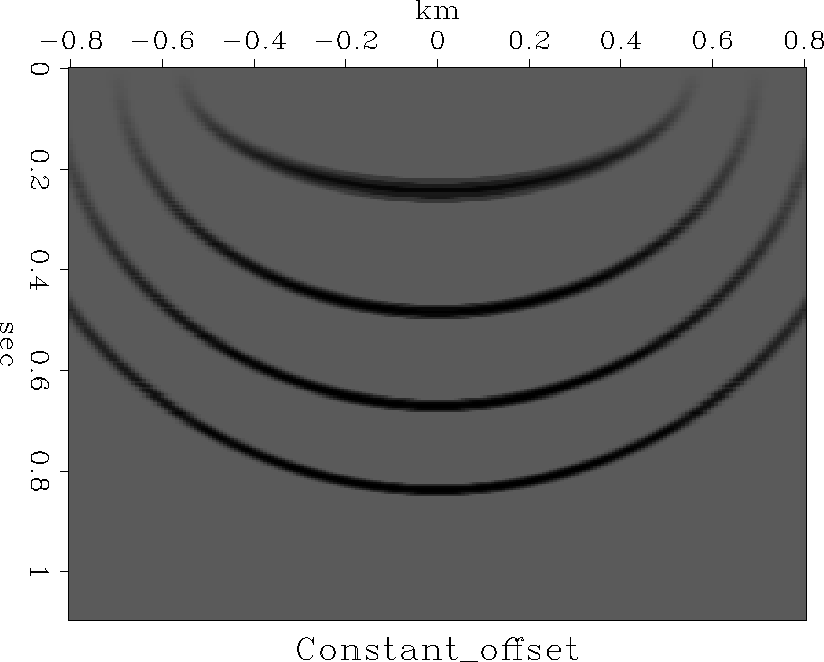
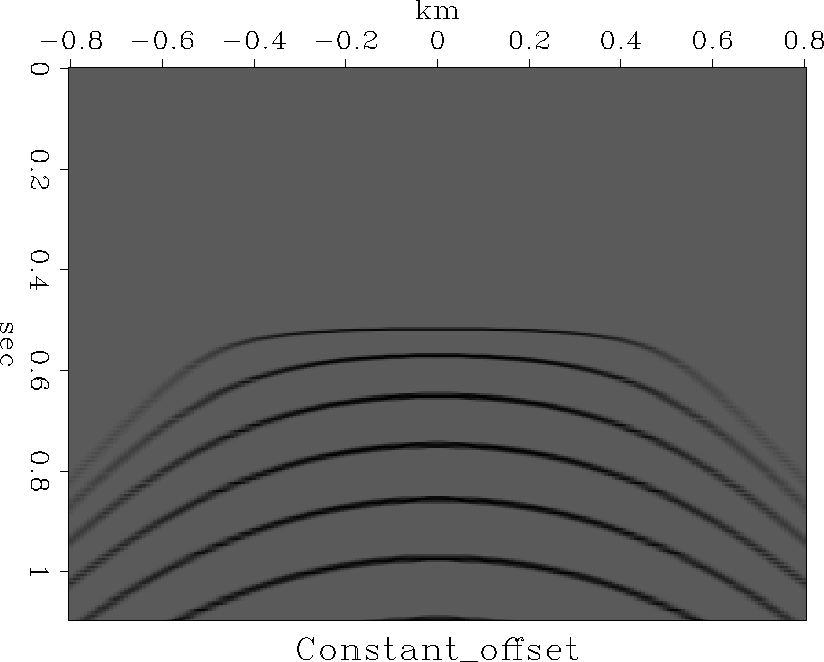
Figure 4
Migrating impulses on a constant-offset section
with subroutine flathyp().
Notice that shallow impulses
(shallow compared to h)
appear ellipsoidal
while deep ones appear circular.
|
|  |





Cos.0
Figure 5
Forward modeling
from an earth impulse with subroutine flathyp().
|
|  |





It is not easy to show that equation (5) can be
cast in the standard mathematical form of an ellipse, namely,
a stretched circle.
But the result is a simple one,
and an important one for later analysis.
Feel free to skip forward over the following verification
of this ancient wisdom.
To help reduce algebraic verbosity,
define a new y equal to the old one shifted by y0.
Also make the definitions
| 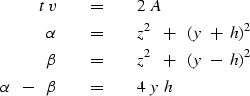 |
(7) |
| |
| |
| |
With these definitions, (5) becomes
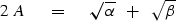
Square to get a new equation with only one square root.
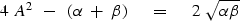
Square again to eliminate the square root.
Introduce definitions of  and
and 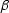 .
.
![\begin{displaymath}
16\ A^4 \ \ -\ \ 8\ A^2 \ [\,2\,z^2 \ +\ 2\,y^2 \ +\ 2\,h^2 ] \ \ +\ \
16\ y^2 \, h^2 \ \eq \ 0 \end{displaymath}](img14.gif)
Bring y and z to the right.
| 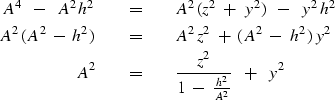 |
|
| |
| (8) |
Finally, recalling all earlier definitions and replacing y by y-y0, we
obtain the canonical form of an ellipse with semi-major axis A and
semi-minor axis B:
| 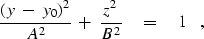 |
(9) |
where
| 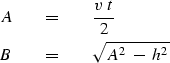 |
(10) |
| (11) |
Fixing t, equation (9) is the equation for a circle with
a stretched z-axis.
The above algebra confirms that the
``string and tack'' definition of an ellipse
matches the ``stretched circle'' definition.
An ellipse in earth model space corresponds
to an impulse on a constant-offset section.





Next: INTRODUCTION TO DIP
Up: PRESTACK MIGRATION
Previous: Prestack migration ellipse
Stanford Exploration Project
12/26/2000
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) is easily prepared
from subroutine kirchfast()
is easily prepared
from subroutine kirchfast() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) by
replacing its hyperbola equation with equation (6).
by
replacing its hyperbola equation with equation (6).