Instead of implementing equation (28) in one step we can split it into two steps. The first step converts raw data at time th to NMOed data at time tn.
| |
(29) |
The second step is the DMO step which like Kirchhoff migration itself is a convolution over the x-axis (or b-axis) with
| |
(30) |
Now the program. Backsolving equation (30) for tn gives
| |
(31) |
Like subroutine flathyp()
if( h**2 <= b**2 ) next
t= sqrt( z**2 / (1-b**2/h**2) )
amp= sqrt(t) * dx/h
if( velhalf*abs(b) * t*t > h**2*z) break
it = 1.5 + (t - t0) / dt
if( it > nt ) break
do ix= max0(1, 1-ib), min0(nx, nx-ib)
if( adj == 0 )
data(it,ix+ib) = data(it,ix+ib) + modl(iz,ix ) * amp
else
modl(iz,ix ) = modl(iz,ix ) + data(it,ix+ib) * amp
}
}
return; end
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
our DMO subroutine dmokirch()
,
our DMO subroutine dmokirch() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) is based on
subroutine kirchfast()
is based on
subroutine kirchfast() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
It is just the same,
except where kirchfast() has a hyperbola
we put equation (31).
In the program,
the variable t0 is called z
and the variable th is called t.
Note, that the velocity velhalf does exclusively
occur in the break condition
(which we have failed to derive,
but which is where the circle and ellipse touch at z=0).
.
It is just the same,
except where kirchfast() has a hyperbola
we put equation (31).
In the program,
the variable t0 is called z
and the variable th is called t.
Note, that the velocity velhalf does exclusively
occur in the break condition
(which we have failed to derive,
but which is where the circle and ellipse touch at z=0).
subroutine dmokirch( adj, add, velhalf, h, t0,dt,dx, modl,nt,nx, data)
integer ix,iz,it,ib, adj, add, nt,nx
real amp,t,z,b, velhalf, h, t0,dt,dx, modl(nt,nx),data(nt,nx)
call adjnull( adj, add, modl,nt*nx, data,nt*nx)
if( h == 0) call erexit('h=0')
do ib= -nx, nx { b = dx * ib # b = midpt separation
do iz= 2, nt { z = t0 + dt * (iz-1) # z = zero-offset time
Figures 24 and 25
were made with subroutine dmokirch() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
Notice the big noise reduction over Figure 18.
.
Notice the big noise reduction over Figure 18.
|
dmatt
Figure 24 Impulse response of DMO and NMO | 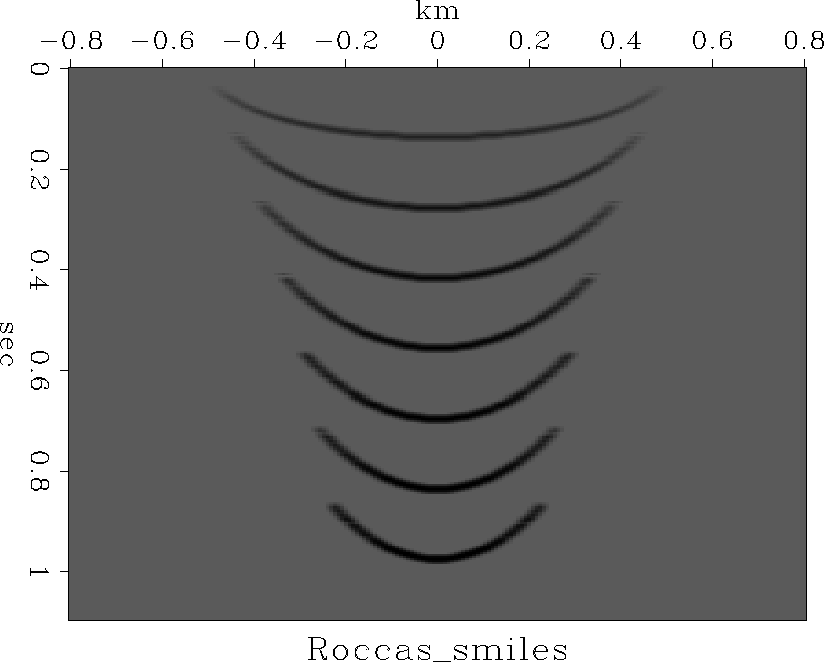 |
|
coffs
Figure 25 Synthetic Cheop's pyramid | 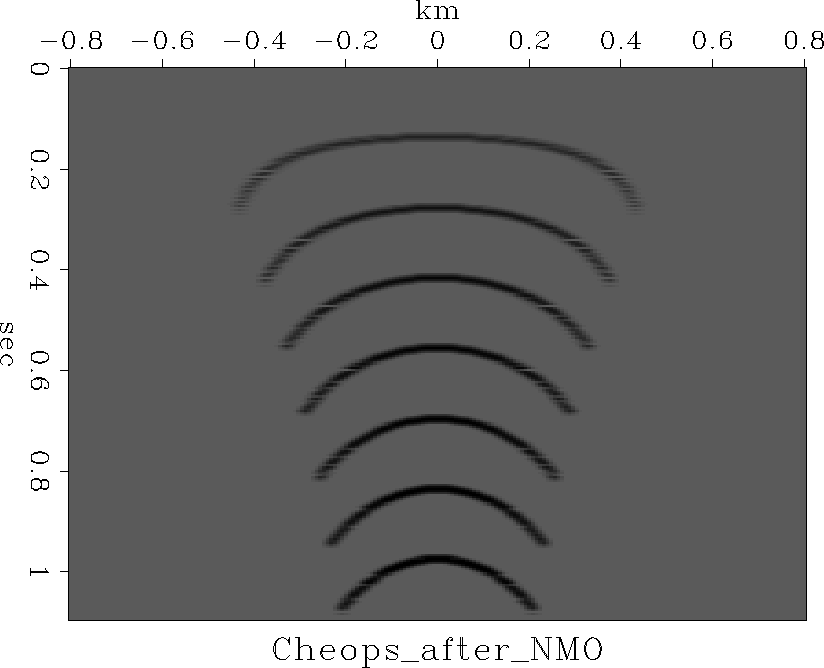 |