The exponential of a causal is causal.

Begin with a causal filter response c_t and its associated C(Z). The Z-transform C(Z) could be evaluated, giving a complex value for each real 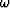$\omega$.This complex value could be exponentiated to get another value, say  

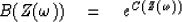$$B(Z(\omega )) \quad = \quad e^{C(Z(\omega ))}$$ (3)

Next, we could inverse transform 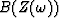$B(Z(\omega ))$ back to b_t. We will prove the amazing fact that b_t must be causal too.

First notice that if C(Z) has no negative powers of Z, then C(Z)² does not either. Likewise for the third power or any positive integer power, or sum of positive integer powers. Now recall the basic power-series definition of the exponential function:  

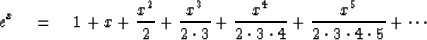$$e^x \quad = \quad1 + x + {x^2 \over 2} + {x^3 \over 2 \cdot ... ...dot 3 \cdot 4} + {x^5 \over 2 \cdot 3 \cdot 4 \cdot 5} + \cdots$$ (4)

Including equation (3) gives the exponential of a causal:   

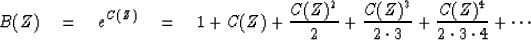$$B(Z) \quad = \quad e^{C(Z)} \quad = \quad1 + C(Z) + {C(Z)^2 ... ...^3 \over 2 \cdot 3} + {C(Z)^4 \over 2 \cdot 3 \cdot 4} + \cdots$$ (5)

Each term in the infinite series corresponds to a causal response, so the sum, b_t, is causal. The factorials in the denominators assure us that the power series always converges, i.e., it is finite for any finite x.) The inverse wavelet to B(Z) is also causal because it is e^-C(Z). (Unfortunately the words ``minimum phase'' distract people from the equivalent property of genuine interest, that the causal wavelet has a causal inverse so we can use feedback filters.)

Putting one polynomial into another or one infinite series into another is an onerous task, even if it does lead to a wavelet that is exactly causal. In practice we do operations that are conceptually the same, but for speed we do them with discrete Fourier transforms. The disadvantage is periodicity, i.e., negative times are represented computationally like negative frequencies. Negative times are the last half of the elements of a vector, so there can be some blurring of late times into negative ones. The subroutine we will use for Fourier transformation is fts()

subroutine fts( signi, nx, rr )
#   complex fourier transform.  if (signi>0) scale = 1; else scale=1/nx
#
#                      nx          signi*2*pi*i*(j-1)*(k-1)/nx
#   rr(k)  =  scale * sum rr(j) * e
#                     j=1             for k=1,2,...,nx=2**integer
#
integer nx, i, j, k, m, istep, pad2
real    signi, arg
complex rr(nx), cmplx, cw, cdel, ct
if( nx != pad2(nx) )    call erexit('fts: nx not a power of 2')
if( signi < 0.)
	do i= 1, nx
		rr(i) = rr(i) / nx
j = 1;  k = 1
do i= 1, nx {
        if (i<=j) { ct = rr(j); rr(j) = rr(i); rr(i) = ct }
        m = nx/2
        while (j>m && m>1) { j = j-m; m = m/2 }         # "&&" means .AND.
        j = j+m
        }
repeat {
        istep = 2*k;   cw = 1.;   arg = signi*3.14159265/k
        cdel = cmplx( cos(arg), sin(arg))
        do m= 1, k {
                do i= m, nx, istep
                        { ct=cw*rr(i+k);  rr(i+k)=rr(i)-ct;  rr(i)=rr(i)+ct }
                cw = cw * cdel
                }
        k = istep
        if(k>=nx) break
	}
return; end

integer function pad2( n )
integer n
pad2 = 1
while( pad2 < n )
        pad2 = pad2 * 2 
return; end