 |
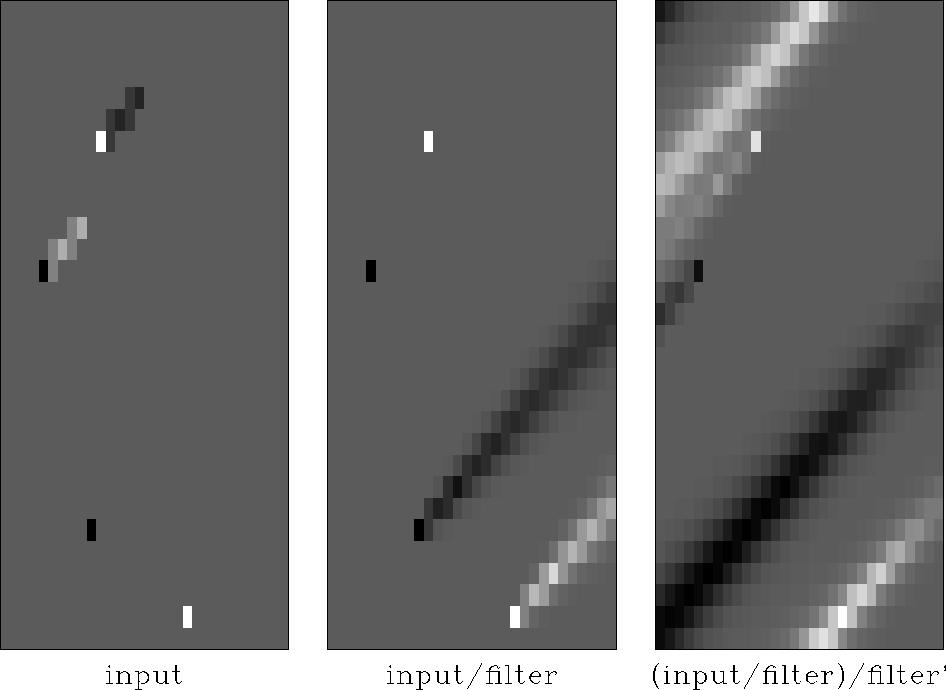
Figure 12 This filter is my guess at a simple low-order 2-D filter whose inverse times its inverse adjoint is approximately a dipping seismic arrival.
Velocity estimation resembles the empty-bin problem because data quality provides us with velocity information in some locations but not in others. Where we have no velocity information, we often have an idea of the orientation of bedding planes or we have other dip information that tells us how to interpolate or smooth velocity between measurement locations. Figure 12
 |
shows how easy it is to use the helix to create directional smoothers. Clapp et.al 1998 demonstrate constructing velocity functions via the helix by the use of directional smoothers or ``flags.'' The space-variable flag filter is introduced as the regularization for a conventional velocity estimation process.
Poststack 3-D wave-equation migration is another area ripe for the helix. When 3-D became important, the finite-difference method declined because we were unable to find rapid solutions to large scale algebraic equations with coefficient matrices like (8). A first question to be asked, however, is whether the helix does anything new that we could not do with Fourier transforms? Certainly, much of the above depends on Fourier transforms, and some could have been done with Fourier transforms. Recursive filtering is often faster than Fourier transforms, but the real contribution of the helix depends on a weakness of Fourier transformation. The frequency domain is great for differential equations with constant coefficients, stationary statistics, and regularly sampled data, but its utility diminishes when these conditions are not met. This theme can be developed further into 3-D poststack migration process that handles 3-D velocity variation in a wave-equation consistent manner Rickett et al. (1998).
Spatial filters easily handle aliased data. Figure 13
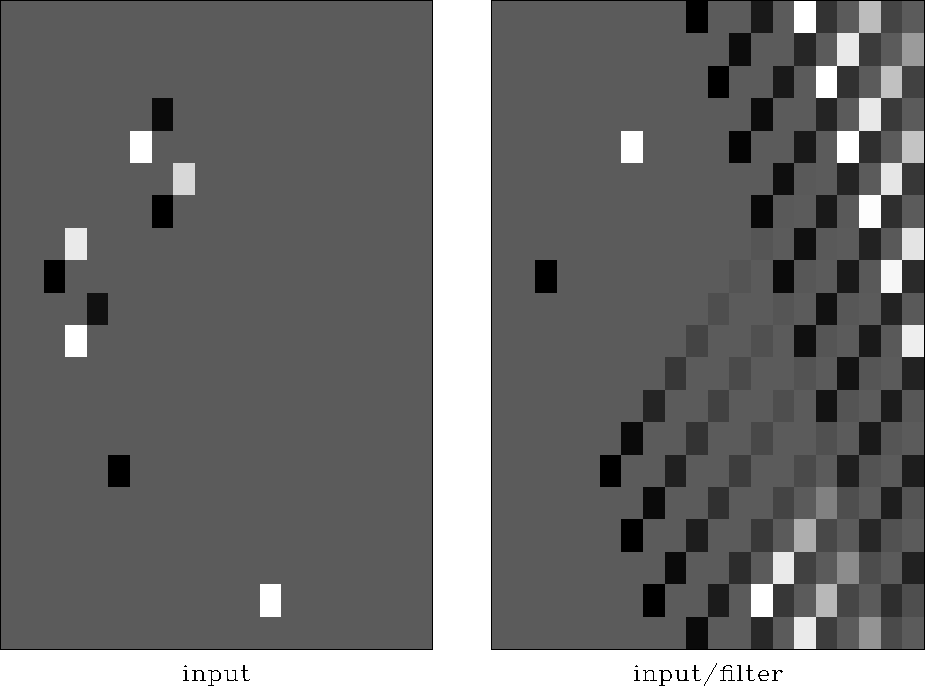 |
shows a filter that destroys two waves, one at the border of aliasing, the other well beyond aliasing. The figure shows that the inverse of such a filter creates aliased plane waves. Claerbout 1992 illustrates synthetic data processing beyond aliasing. Recently Crawley 1998 began demonstrating stacking on field data that is aliased in offset at constant midpoint. Again, the helix should accelerate convergence.