




Next: Further applications
Up: Multidimensional recursive filters via
Previous: Iteratively fitting models to
The basic formulation of a geophysical estimation problem
consists of setting up two goals,
one for data fitting,
and the other for model smoothing.
We have data 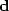 ,a map or model
,a map or model  ,a transformation
and a roughening filter
,a transformation
and a roughening filter 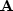 ,like the gradient
,like the gradient 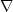 or the helix derivative
or the helix derivative 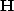 .The two goals may be written as:
.The two goals may be written as:
| 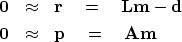 |
(12) |
| (13) |
which defines two residuals,
a data residual  ,and a model residual
,and a model residual 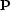 , which
are usually minimized by iterative conjugate-gradient, least-squares methods.
A common case is ``minimum wiggliness''
when
, which
are usually minimized by iterative conjugate-gradient, least-squares methods.
A common case is ``minimum wiggliness''
when 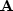 is taken to be the gradient operator.
The gradient is not invertable so we cannot precondition with its inverse.
On the other hand,
since
is taken to be the gradient operator.
The gradient is not invertable so we cannot precondition with its inverse.
On the other hand,
since 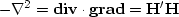 ,taking
,taking 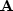 to be the helix derivative
to be the helix derivative 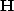 ,we can invert
,we can invert 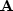 and proceed with the preconditioning:
We change the free variable in the
fitting goals from
and proceed with the preconditioning:
We change the free variable in the
fitting goals from  to
to 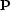 (by inverting (13))
with
(by inverting (13))
with 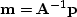 and substituting into both goals getting new goals
and substituting into both goals getting new goals
| 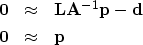 |
(14) |
| (15) |
In my experience,
iterative solvers find convergence much more quickly
when the free variable is the roughened map 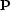 rather than the map
rather than the map  itself.
itself.
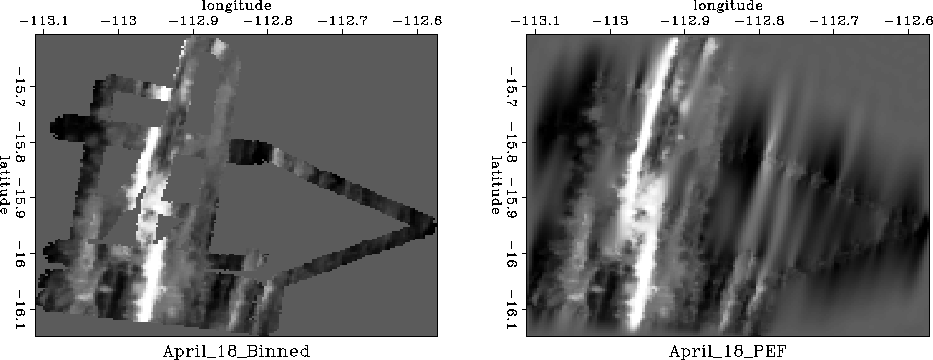
Figure 11 (left) shows ocean depth
measured by a Seabeam apparatus.
seapef
Figure 11
Filling empty bins with a prediction-error filter.

Locations not surveyed are evident as the homogeneous gray area.
Using a process akin to ``blind deconvolution'' a
2-D prediction error filter 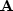 is found.
Then missing data values are estimated and shown on the right.
Preconditioning with the helix speeded this estimation by a factor of about 30.
The figure required a few seconds of calculation for about 105 unknowns.
is found.
Then missing data values are estimated and shown on the right.
Preconditioning with the helix speeded this estimation by a factor of about 30.
The figure required a few seconds of calculation for about 105 unknowns.





Next: Further applications
Up: Multidimensional recursive filters via
Previous: Iteratively fitting models to
Stanford Exploration Project
6/2/1998
![]() is found.
Then missing data values are estimated and shown on the right.
Preconditioning with the helix speeded this estimation by a factor of about 30.
The figure required a few seconds of calculation for about 105 unknowns.
is found.
Then missing data values are estimated and shown on the right.
Preconditioning with the helix speeded this estimation by a factor of about 30.
The figure required a few seconds of calculation for about 105 unknowns.