




Next: Matrix view of the
Up: Multidimensional recursive filters via
Previous: Examples of simple 2-d
The function
| 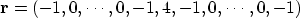 |
(4) |
is an autocorrelation function.
It is symmetrical about the ``4'' and its Fourier transform
is positive for all frequencies.
Digging out an old textbook Claerbout (1976),
we discover
how to compute a causal wavelet with this autocorrelation.
I used the ``Kolmogoroff spectral-factorization method''
to find this wavelet 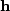 :
:
| 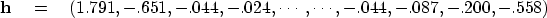 |
(5) |
Wind the signal  around a
vertical-axis helix to see its two-dimensional shape
around a
vertical-axis helix to see its two-dimensional shape 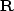 :
:
| ![\begin{displaymath}
\bold R \quad = \quad
\left[
\begin{array}
{rrr}
& -1 & \\ -1 & 4 & -1 \\ & -1 &
\end{array}\right]\end{displaymath}](img28.gif) |
(6) |
This 2-D filter is
is the negative of the finite-difference representation
of the negative of the Laplacian operator, generally denoted
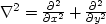 .Now wind the signal
.Now wind the signal 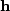 around the same helix
to see its two-dimensional shape
around the same helix
to see its two-dimensional shape 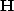 :
:
| ![\begin{displaymath}
\bold H \quad = \quad
\left[
\begin{array}
{rrrrrrrrr}
& ...
...ots &-.044 & -.087 & -.200 & -.558 & & & &
\end{array} \right]\end{displaymath}](img31.gif) |
(7) |
In the 2-D representation (7)
we see the coefficients diminishing rapidly away from maximum value 1.791.
My claim is that the 2-D autocorrelation of (7)
is (6).
You verified this idea
at the beginning of this paper where the numbers were all ones.
You can check it again in a few moments
if you drop the small values, say 0.2 and smaller.
Since
the autocorrelation of 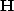 is
is
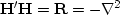 is a second derivative,
the operator
is a second derivative,
the operator 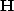 must be something like a first derivative.
As a geophysicist, I found it natural to compare
the operator
must be something like a first derivative.
As a geophysicist, I found it natural to compare
the operator 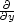 to
to 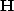 by applying them to a local topographic map.
The result shown in
Figure 9
is that
by applying them to a local topographic map.
The result shown in
Figure 9
is that 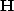 enhances drainage patterns whereas
enhances drainage patterns whereas
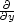 enhances mountain ridges.
enhances mountain ridges.
helocut
Figure 9
(a) Topography,
(b) helical derivative,
(c) slope south.

Our construction makes 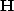 have the energy spectrum kx2+ky2,
so the magnitude of its Fourier transform is
have the energy spectrum kx2+ky2,
so the magnitude of its Fourier transform is 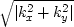 .This rotationally invariant function in the Fourier domain
contrasts sharply with the nonrotationally invariant
function shape in (x,y)-space.
The difference must arise from the phase spectrum.
The factorization (7)
is nonunique in that causality
associated with the helix mapping
can be defined along either x or y axes;
thus the operator
(7)
can be rotated or reflected.
.This rotationally invariant function in the Fourier domain
contrasts sharply with the nonrotationally invariant
function shape in (x,y)-space.
The difference must arise from the phase spectrum.
The factorization (7)
is nonunique in that causality
associated with the helix mapping
can be defined along either x or y axes;
thus the operator
(7)
can be rotated or reflected.
The operator 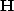 has
curious similarities and differences
with the familiar gradient and divergence operators.
In two-dimensional physical space,
the gradient maps one field to two fields
(north slope and east slope).
The factorization of
has
curious similarities and differences
with the familiar gradient and divergence operators.
In two-dimensional physical space,
the gradient maps one field to two fields
(north slope and east slope).
The factorization of 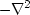 with the helix
gives us the operator
with the helix
gives us the operator 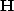 that maps one field to one field.
Being a one-to-one transformation
(unlike gradient and divergence)
the operator
that maps one field to one field.
Being a one-to-one transformation
(unlike gradient and divergence)
the operator 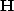 is potentially invertible
by deconvolution (recursive filtering).
is potentially invertible
by deconvolution (recursive filtering).
I have chosen the name![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) ``helix derivative''
or ``helical derivative'' for the operator
``helix derivative''
or ``helical derivative'' for the operator 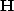 .A telephone pole has a narrow shadow behind it.
The helix integral (middle frame of Figure 10)
and the helix derivative (left frame)
show shadows with an angular bandwidth approaching
.A telephone pole has a narrow shadow behind it.
The helix integral (middle frame of Figure 10)
and the helix derivative (left frame)
show shadows with an angular bandwidth approaching 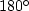 .Thus,
.Thus, 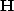 is much less directional than either
is much less directional than either
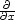 or
or
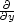 .
.
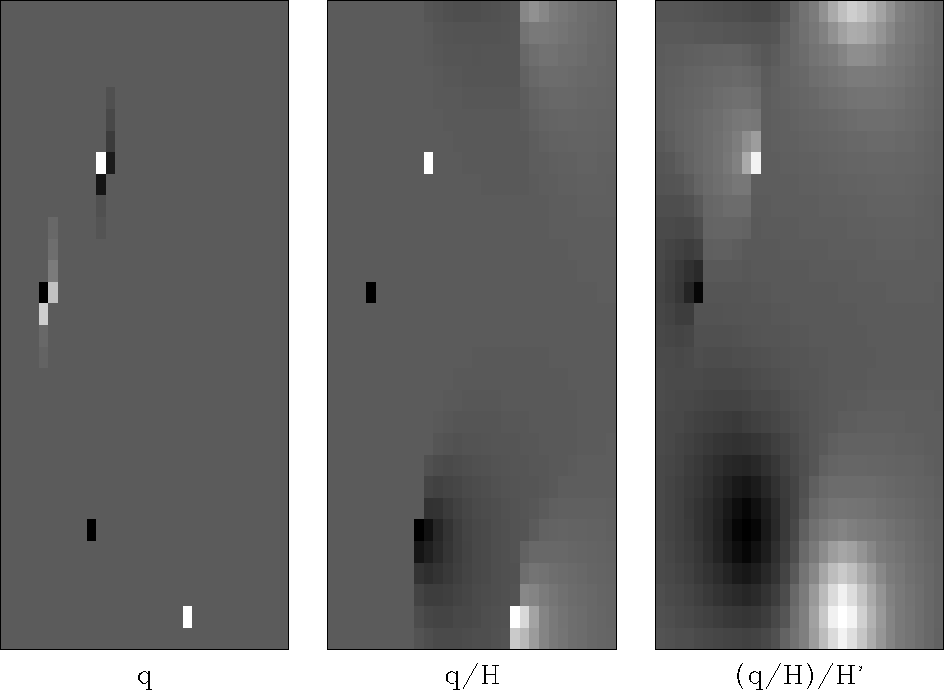
lapfac
Figure 10
Deconvolution by a filter whose autocorrelation
is the two-dimensional Laplacian operator.
Amounts to solving the Poisson equation.
Left is 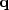 ; Middle is
; Middle is 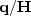 ; Right is
; Right is 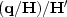 .
.

This is where the story all comes together.
One-dimensional theory, such as the Kolmogoroff spectral factorization,
produces not merely a causal wavelet
with the required autocorrelation.
It produces a wavelet that is stable in deconvolution.
Using 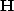 in one-dimensional polynomial division,
we can solve many formerly difficult problems very rapidly.
Consider the Laplace equation with sources (Poisson's equation).
Polynomial division and its reverse (adjoint) gives us
in one-dimensional polynomial division,
we can solve many formerly difficult problems very rapidly.
Consider the Laplace equation with sources (Poisson's equation).
Polynomial division and its reverse (adjoint) gives us
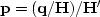 which means that we have solved
which means that we have solved
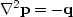 in Figure 10
by using polynomial division on a helix.
Using the seven coefficients shown,
the cost is fourteen multiplications
(because we need to run both ways) per mesh point.
in Figure 10
by using polynomial division on a helix.
Using the seven coefficients shown,
the cost is fourteen multiplications
(because we need to run both ways) per mesh point.





Next: Matrix view of the
Up: Multidimensional recursive filters via
Previous: Examples of simple 2-d
Stanford Exploration Project
6/2/1998
![\begin{displaymath}
\bold R \quad = \quad
\left[
\begin{array}
{rrr}
& -1 & \\ -1 & 4 & -1 \\ & -1 &
\end{array}\right]\end{displaymath}](img28.gif)
![]() is
is
![]() is a second derivative,
the operator
is a second derivative,
the operator ![]() must be something like a first derivative.
As a geophysicist, I found it natural to compare
the operator
must be something like a first derivative.
As a geophysicist, I found it natural to compare
the operator ![]() to
to ![]() by applying them to a local topographic map.
The result shown in
Figure 9
is that
by applying them to a local topographic map.
The result shown in
Figure 9
is that ![]() enhances drainage patterns whereas
enhances drainage patterns whereas
![]() enhances mountain ridges.
enhances mountain ridges.

![]() have the energy spectrum kx2+ky2,
so the magnitude of its Fourier transform is
have the energy spectrum kx2+ky2,
so the magnitude of its Fourier transform is ![]() .This rotationally invariant function in the Fourier domain
contrasts sharply with the nonrotationally invariant
function shape in (x,y)-space.
The difference must arise from the phase spectrum.
The factorization (7)
is nonunique in that causality
associated with the helix mapping
can be defined along either x or y axes;
thus the operator
(7)
can be rotated or reflected.
.This rotationally invariant function in the Fourier domain
contrasts sharply with the nonrotationally invariant
function shape in (x,y)-space.
The difference must arise from the phase spectrum.
The factorization (7)
is nonunique in that causality
associated with the helix mapping
can be defined along either x or y axes;
thus the operator
(7)
can be rotated or reflected.
![]() has
curious similarities and differences
with the familiar gradient and divergence operators.
In two-dimensional physical space,
the gradient maps one field to two fields
(north slope and east slope).
The factorization of
has
curious similarities and differences
with the familiar gradient and divergence operators.
In two-dimensional physical space,
the gradient maps one field to two fields
(north slope and east slope).
The factorization of ![]() with the helix
gives us the operator
with the helix
gives us the operator ![]() that maps one field to one field.
Being a one-to-one transformation
(unlike gradient and divergence)
the operator
that maps one field to one field.
Being a one-to-one transformation
(unlike gradient and divergence)
the operator ![]() is potentially invertible
by deconvolution (recursive filtering).
is potentially invertible
by deconvolution (recursive filtering).
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) ``helix derivative''
or ``helical derivative'' for the operator
``helix derivative''
or ``helical derivative'' for the operator ![]() .A telephone pole has a narrow shadow behind it.
The helix integral (middle frame of Figure 10)
and the helix derivative (left frame)
show shadows with an angular bandwidth approaching
.A telephone pole has a narrow shadow behind it.
The helix integral (middle frame of Figure 10)
and the helix derivative (left frame)
show shadows with an angular bandwidth approaching ![]() .Thus,
.Thus, ![]() is much less directional than either
is much less directional than either
![]() or
or
![]() .
.
![]() in one-dimensional polynomial division,
we can solve many formerly difficult problems very rapidly.
Consider the Laplace equation with sources (Poisson's equation).
Polynomial division and its reverse (adjoint) gives us
in one-dimensional polynomial division,
we can solve many formerly difficult problems very rapidly.
Consider the Laplace equation with sources (Poisson's equation).
Polynomial division and its reverse (adjoint) gives us
![]() which means that we have solved
which means that we have solved
![]() in Figure 10
by using polynomial division on a helix.
Using the seven coefficients shown,
the cost is fourteen multiplications
(because we need to run both ways) per mesh point.
in Figure 10
by using polynomial division on a helix.
Using the seven coefficients shown,
the cost is fourteen multiplications
(because we need to run both ways) per mesh point.