




Next: Conjugate Gradient Definition
Up: Review of Frequency-domain waveform
Previous: The Inverse Problem
Methods for calculating the gradient without explicitly computing the partial derivatives of the data are well established Lailly (1983); Pratt et al. (1998); Pratt and Worthington (1989); Tarantola (1984). The main result in the time-domain inversion literature is that the gradient vector can be computed by a zero-lag correlation of the wavefield propagated forward from the source point, 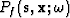 , and the residual wavefield propagated backwards from the farthest receiver location toward the source point past each successive receiver,
, and the residual wavefield propagated backwards from the farthest receiver location toward the source point past each successive receiver, 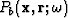 . The frequency-domain equivalent to this zero-lag correlation is the multiplication of these two wavefields according to
. The frequency-domain equivalent to this zero-lag correlation is the multiplication of these two wavefields according to
| 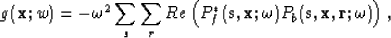 |
(6) |
where Re indicates the real component of the multiplication result. The summation over sources and receivers is done for each non-linear iteration at each frequency. Following Sirgue and Pratt (2004) in assuming a point source of unit amplitude and zero phase, the forward-propagated wavefield Pf is given by
| 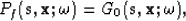 |
(7) |
while back-propagated wavefield Pb is defined by
| 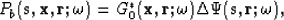 |
(8) |
where 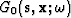 and
and 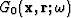 represent the monochromatic Green's functions for an excitation at the source and receiver points in the medium, respectively. Hence, the full gradient vector expression is
represent the monochromatic Green's functions for an excitation at the source and receiver points in the medium, respectively. Hence, the full gradient vector expression is
| 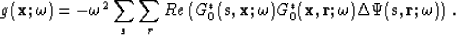 |
(9) |
Note that 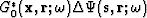 represents the back-projection of the data residuals and is similar to a "migration with the residual wavefield data" Mora (1987).
represents the back-projection of the data residuals and is similar to a "migration with the residual wavefield data" Mora (1987).





Next: Conjugate Gradient Definition
Up: Review of Frequency-domain waveform
Previous: The Inverse Problem
Stanford Exploration Project
1/16/2007