




Next: Terzaghi's model
Up: Alternative rock velocity models
Previous: Alternative rock velocity models
Biot's theory Bourbie et al. (1987)
is based on the fundamental assumption of continuum mechanics
that the wavelength is large in comparison with the size of the
macroscopic elementary volume of the material and
that the displacement is small so that the strain tensor is linear.
These continuum conditions are readily satisfied by seismic studies.
Furthermore, Biot assumes
that the rock matrix is elastic and isotropic,
that the liquid phase is continuous,
that the rock matrix is solid,
that the pores are disconnected![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) ,
and
that the porosity is isotropic and uniform.
These assumptions are approximately true for many subsurface rocks.
,
and
that the porosity is isotropic and uniform.
These assumptions are approximately true for many subsurface rocks.
The equation of continuity for a porous rock is
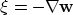
where 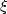 is the local fluid increase due to the filtration
of fluid
is the local fluid increase due to the filtration
of fluid 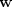 .
If
.
If 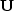 is the displacement of the liquid phase
and
is the displacement of the liquid phase
and 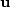 is the displacement of the solid phase, then
the filtration velocity is
is the displacement of the solid phase, then
the filtration velocity is
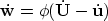
where 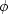 is the rock porosity.
is the rock porosity.
The constitutive equation is
| 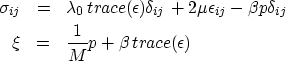 |
(25) |
| (26) |
where 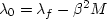 .The coefficient
.The coefficient 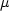 is the standard shear modulus, which
is independent of the fluid content.
The coefficient
is the standard shear modulus, which
is independent of the fluid content.
The coefficient 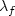 is the second Lame coefficient for a closed
rock sample - a rock sample filled with water and without any change in
fluid contents (
is the second Lame coefficient for a closed
rock sample - a rock sample filled with water and without any change in
fluid contents (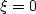 ).
Consequently,
).
Consequently, 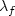 is linked to the elastic constants of the rock
matrix and the fluid.
is linked to the elastic constants of the rock
matrix and the fluid. 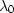 is the analogue coefficient for
an open system - a system with no external pressure (p = 0).
Coefficient M is the pressure required to increase the fluid
content of a unit volume at isovolumetric strain -
is the analogue coefficient for
an open system - a system with no external pressure (p = 0).
Coefficient M is the pressure required to increase the fluid
content of a unit volume at isovolumetric strain - 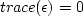 .The coefficient
.The coefficient 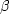 quantifies the proportion of pressure due
to the variation in fluid content for an open system. It is linked to
the porosity and the geometry of the flow channels.
All these coefficients can be measured in the laboratory
on rock samples.
In the limiting case that
quantifies the proportion of pressure due
to the variation in fluid content for an open system. It is linked to
the porosity and the geometry of the flow channels.
All these coefficients can be measured in the laboratory
on rock samples.
In the limiting case that 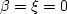 and
and 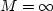 we yield
the constitutive relationship for a single solid phase.
we yield
the constitutive relationship for a single solid phase.
The constitutive equation is derived from changes in
the volumetric energy potential V due to infinitesimal increments
in strain and fluid contents
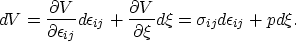
where
p is a pressure average in the fluid,
sigma is the macroscopic stress tensor.
The isotropy of the rock permits an approximation of the general
tensor relation by the tensors first two invariants (the tensor's
trace is the first invariant).
Introduction of the standard Lame coefficients yields the constitutive
relation above.
The constitutive equation at zero fluid pressure p = 0
and at hydrostatic fluid pressure 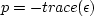 yields
relationships that when expressed in terms of
the saturated bulk modulo Ks,
the open or dry bulk modulo Kd,
the bulk modulo of the fluid Kf, and
the bulk modulo of the solid skeleton Km
can be combined to the Gassmann equation 15.
The equations assume quasi-static behaviour and are only true
for low-frequency waves.
yields
relationships that when expressed in terms of
the saturated bulk modulo Ks,
the open or dry bulk modulo Kd,
the bulk modulo of the fluid Kf, and
the bulk modulo of the solid skeleton Km
can be combined to the Gassmann equation 15.
The equations assume quasi-static behaviour and are only true
for low-frequency waves.
The equations of motion
for porous rocks are
| 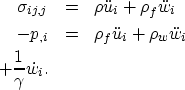 |
(27) |
| |
| (28) |
where
 is the stress,
u is the displacement of the matrix,
w is the displacement of the fluid,
is the stress,
u is the displacement of the matrix,
w is the displacement of the fluid,
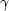 is the effective transmissibility
(or hydraulic permeability or fluid mobility).
The transmissibility is the ratio of the
absolute rock permeability k and the fluid viscosity
is the effective transmissibility
(or hydraulic permeability or fluid mobility).
The transmissibility is the ratio of the
absolute rock permeability k and the fluid viscosity 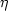 :
: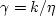 .The average density
.The average density 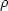 is
is 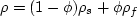 .
The effective fluid density
.
The effective fluid density 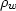 takes the porosity
and the shape of the pores into account.
The coupling effect is usually described by
takes the porosity
and the shape of the pores into account.
The coupling effect is usually described by
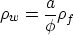
where the tortuosity parameter 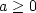 is the factor incorporating
the pore shape. Tortuosity tends to 1 as the porosity tends to 1.
Berryman 1980 suggested to apply
the tortuosity expression for solid spherical particles
is the factor incorporating
the pore shape. Tortuosity tends to 1 as the porosity tends to 1.
Berryman 1980 suggested to apply
the tortuosity expression for solid spherical particles
![\begin{displaymath}
a = \frac{1}{2} [\frac{1}{\phi} + 1]\end{displaymath}](img102.gif)
to porous rock.
If there is no average relative fluid movement with respect to the
overall macroscopic movement of the rock, i.e. 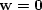 ,
then the first equation of 28 is reduced to the
standard single phase case.
If the acceleration of the fluid and the rock are zero -
,
then the first equation of 28 is reduced to the
standard single phase case.
If the acceleration of the fluid and the rock are zero -
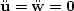 -
the motion is a steady state flow and the second
equation of 28 reduces to Darcy's classic law of
fluid flow in permeable material.
-
the motion is a steady state flow and the second
equation of 28 reduces to Darcy's classic law of
fluid flow in permeable material.
Bourlie 1987 derives
The equations of motion from a strain potential expression
that yields the constitutive equation,
a potential expression for dissipation, and
a potential expression for kinetic energy.
Biot's wave equation is, as usual, derived by substitution
from the equation of motion 28 and
the constitutive equation 26:
| 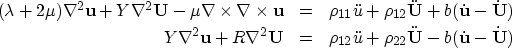 |
(29) |
| |
where
| 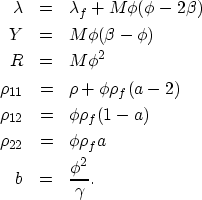 |
|
| |
| |
| (30) |
| |
| |
| |
b is the coefficient governing the wave's energy dissipation
which in Biot's system is entirely due to relative motion of the
fluid and matrix components.
The equations reduce to the limiting case of a perfect fluid when
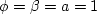 ,
, 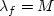 , and
, and 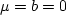 (since
(since
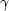 tends to infinity and the viscosity tends to ).
Consequently, the first equation disappears of 30 and
the second reduces
to
tends to infinity and the viscosity tends to ).
Consequently, the first equation disappears of 30 and
the second reduces
to
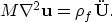
If the medium is solid, we have 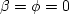 and a tends to
infinity. Consequently, the second equation of 30 yields
and a tends to
infinity. Consequently, the second equation of 30 yields
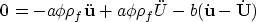
while the first equation reduces to
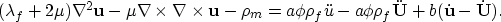
The right-hand-side term of the two equations are equal.
Consequently, the left hand expression of the second equation is zero,
which is the standard wave equation for single phase solids.
Without Dissipation -
b=0 which implies
transmissibility 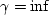 or
porosity
or
porosity 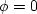 -
Biot's wave equation for porous rocks predicts
two P-waves.
For P-waves we can express the displacements
-
Biot's wave equation for porous rocks predicts
two P-waves.
For P-waves we can express the displacements 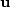 and
and 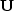 as
gradients of a potential
as
gradients of a potential 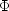 :
:
| ![\begin{displaymath}
\left[
\begin{array}
{c}
{\bf u} \\ {\bf U}\end{array}\right...
... \Phi} \\ {\nabla \Phi}\end{array}\right]
= \nabla {\bf \Phi}.\end{displaymath}](img116.gif) |
(31) |
Consequently, 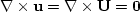 and the wave equation expressions 30 reduce to
and the wave equation expressions 30 reduce to
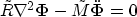
where
![\begin{displaymath}
\tilde{R} =
\left[
\begin{array}
{cc}
\lambda + 2 \mu & Y \...
...o_{11} & \rho_{12} \\ \rho_{12} & \rho_{22} \end{array}\right].\end{displaymath}](img119.gif)
The matrix 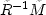 is positive definite and
consequently has two real eigenvalues vp1 and vp2.
In the matrix's eigenvector reference system, the wave
equation reduces to
is positive definite and
consequently has two real eigenvalues vp1 and vp2.
In the matrix's eigenvector reference system, the wave
equation reduces to
![\begin{displaymath}
\nabla^2 {\bf \Phi^\star}
-
\left[
\begin{array}
{cc}
\fra...
...& \frac{1}{v_{p2}}\end{array}\right]
\ddot{\bf \Phi}^\star
= 0\end{displaymath}](img121.gif)
where 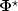 is the potential function in the eigenvector
reference system.
The equation implies two decoupled P-waves. The second P-wave velocity
vp2 is usually significantly smaller than the first. The faster
vp1 merges with the classic P-wave in the absence of pore fluids.
is the potential function in the eigenvector
reference system.
The equation implies two decoupled P-waves. The second P-wave velocity
vp2 is usually significantly smaller than the first. The faster
vp1 merges with the classic P-wave in the absence of pore fluids.
Analogues
introducing shear waves
| ![\begin{displaymath}
\left[
\begin{array}
{c}
{\bf u} \\ {\bf U}\end{array}\right...
...\times \Theta}\end{array}\right]
= \nabla \times {\bf \Theta}.\end{displaymath}](img123.gif) |
(32) |
we find a single shear wave with velocity
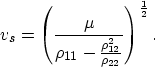
The fluid influences the shear velocity indirectly due to its effect
on the overall inertia of the porous rock.
With dissipation
the P-Wave ansatz 31 reduces
the general wave equation 30
to
| 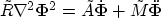 |
(33) |
where  is the damping matrix
is the damping matrix
![\begin{displaymath}
\tilde{A} =
\left[
\begin{array}
{cc}
b & -b \\ -b & b\end{array}\right].\end{displaymath}](img127.gif)
The ansatz for harmonic P-waves is
| 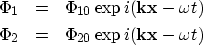 |
(34) |
| (35) |
where 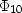 and
and 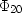 are constant and
are constant and  and
and 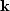 are the angular frequency and the wave number.
The introduction of this ansatz into the wave equation
are the angular frequency and the wave number.
The introduction of this ansatz into the wave equation ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) yields a system of two equation. To ensure that a solution exists the
determinant of the homogeneous system has to be zero. This condition
leads to dispersion relationships with two solutions: kP1 and
kP2 which relate to the two types of P-waves found in the
case without dissipation. Both wave numbers are complex.
The real part describes the harmonic propagation:
yields a system of two equation. To ensure that a solution exists the
determinant of the homogeneous system has to be zero. This condition
leads to dispersion relationships with two solutions: kP1 and
kP2 which relate to the two types of P-waves found in the
case without dissipation. Both wave numbers are complex.
The real part describes the harmonic propagation:
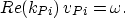
where vPi relates to the velocities found in the non-dissipating
discussion.
The
complex part governs the amplitude dissipation of the wave.
The propagation velocity is dispersive since frequency dependent.
As the frequency approaches zero, the source of dissipation - the
relative motion between the fluid and the matrix - vanishes.
At frequencies where 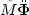 can be ignored,
the equation, once more, reduces to Darcy's law of steady flow.
can be ignored,
the equation, once more, reduces to Darcy's law of steady flow.
In summary, Biot's model yields a consistent and analytic solution
to the propagation of waves in porous media. Its results are backed
by laboratory confirmations at a wide variety of rock samples.
Unfortunately, its velocity expressions are rather complicated.





Next: Terzaghi's model
Up: Alternative rock velocity models
Previous: Alternative rock velocity models
Stanford Exploration Project
3/9/1999
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) ,
and
that the porosity is isotropic and uniform.
These assumptions are approximately true for many subsurface rocks.
,
and
that the porosity is isotropic and uniform.
These assumptions are approximately true for many subsurface rocks.
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) ,
and
that the porosity is isotropic and uniform.
These assumptions are approximately true for many subsurface rocks.
,
and
that the porosity is isotropic and uniform.
These assumptions are approximately true for many subsurface rocks.
![]()
![]()
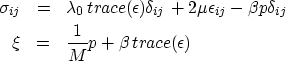
![]()
![]() yields
relationships that when expressed in terms of
the saturated bulk modulo Ks,
the open or dry bulk modulo Kd,
the bulk modulo of the fluid Kf, and
the bulk modulo of the solid skeleton Km
can be combined to the Gassmann equation 15.
The equations assume quasi-static behaviour and are only true
for low-frequency waves.
yields
relationships that when expressed in terms of
the saturated bulk modulo Ks,
the open or dry bulk modulo Kd,
the bulk modulo of the fluid Kf, and
the bulk modulo of the solid skeleton Km
can be combined to the Gassmann equation 15.
The equations assume quasi-static behaviour and are only true
for low-frequency waves.
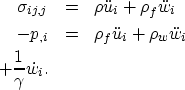
![]()
![]()
![]() ,
then the first equation of 28 is reduced to the
standard single phase case.
If the acceleration of the fluid and the rock are zero -
,
then the first equation of 28 is reduced to the
standard single phase case.
If the acceleration of the fluid and the rock are zero -
![]() -
the motion is a steady state flow and the second
equation of 28 reduces to Darcy's classic law of
fluid flow in permeable material.
-
the motion is a steady state flow and the second
equation of 28 reduces to Darcy's classic law of
fluid flow in permeable material.
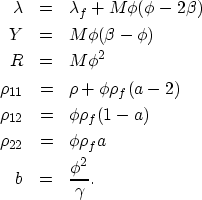
![]() ,
, ![]() , and
, and ![]() (since
(since
![]() tends to infinity and the viscosity tends to ).
Consequently, the first equation disappears of 30 and
the second reduces
to
tends to infinity and the viscosity tends to ).
Consequently, the first equation disappears of 30 and
the second reduces
to
![]()
![]()
![]()
![]() or
porosity
or
porosity ![]() -
Biot's wave equation for porous rocks predicts
two P-waves.
For P-waves we can express the displacements
-
Biot's wave equation for porous rocks predicts
two P-waves.
For P-waves we can express the displacements ![]() and
and ![]() as
gradients of a potential
as
gradients of a potential ![]() :
:
![]()
![]()
![\begin{displaymath}
\nabla^2 {\bf \Phi^\star}
-
\left[
\begin{array}
{cc}
\fra...
...& \frac{1}{v_{p2}}\end{array}\right]
\ddot{\bf \Phi}^\star
= 0\end{displaymath}](img121.gif)
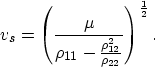
![]()
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) yields a system of two equation. To ensure that a solution exists the
determinant of the homogeneous system has to be zero. This condition
leads to dispersion relationships with two solutions: kP1 and
kP2 which relate to the two types of P-waves found in the
case without dissipation. Both wave numbers are complex.
The real part describes the harmonic propagation:
yields a system of two equation. To ensure that a solution exists the
determinant of the homogeneous system has to be zero. This condition
leads to dispersion relationships with two solutions: kP1 and
kP2 which relate to the two types of P-waves found in the
case without dissipation. Both wave numbers are complex.
The real part describes the harmonic propagation:
![]()