




Next: Vectors
Up: Schwab & Schroeder: Algebraic
Previous: Schwab & Schroeder: Algebraic
To introduce Jest we will discuss what probably is
the Hello World program
of image processing: image restoration by deconvolution.
Many physical transmission systems blur their input signal.
For example, atmospheric turbulences blur
satellite and telescope images.
The broadband wavelet in a seismic experiment blurs
the reflectivity series of the Earth.
Instruments themselves cause a degradation of their input
which often is well described by a blur.
Mathematically,
a blurred image y(t) is usually
modeled as the convolution of the original image f(t)
by a blurring filter b(t):
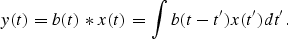
If the image is digitized, convolution can be expressed discretely as
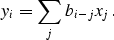
The discrete version can be formulated as a matrix multiplication
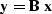 :
:
![\begin{displaymath}
\left[
\begin{array}
{c}
y_1 \\ y_2 \\ y_3 \\ y_4 \\ y_5 \\ ...
...n{array}
{c}
x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5 \end{array}\right]\end{displaymath}](img4.gif)
which in this case implements transient boundary conditions.
In our example, we deconvolve
the time series 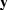 recorded by a seismograph with known
blur filter
recorded by a seismograph with known
blur filter 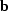 .
To estimate the unblurred image
.
To estimate the unblurred image  , we seek the
unconstrained minimum of
, we seek the
unconstrained minimum of
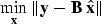
which yields the least square solution
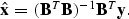
The routine that deconvolves the time series combines
Jest vectors that represent 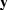 ,
, 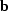 and
and 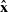 ,
a Jest linear-operator-with-adjoint to implement the convolution
,
a Jest linear-operator-with-adjoint to implement the convolution 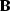 ,
and finally Jest's conjugate-gradient solver to estimate the solution
vector
,
and finally Jest's conjugate-gradient solver to estimate the solution
vector 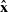 .
Figure 1 shows
the known filter,
the blurred input time series,
and the deconvolved result.
.
Figure 1 shows
the known filter,
the blurred input time series,
and the deconvolved result.
tcai
Figure 1
Seismogram deconvolution.
The top signal is the known filter.
The second signal is the received, blurred signal.
The third signal is the deblurred signal estimated from the signals above.
The bottom signal is the correct answer.










Next: Vectors
Up: Schwab & Schroeder: Algebraic
Previous: Schwab & Schroeder: Algebraic
Stanford Exploration Project
3/8/1999
![]()
![]()
![\begin{displaymath}
\left[
\begin{array}
{c}
y_1 \\ y_2 \\ y_3 \\ y_4 \\ y_5 \\ ...
...n{array}
{c}
x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5 \end{array}\right]\end{displaymath}](img4.gif)
![]() recorded by a seismograph with known
blur filter
recorded by a seismograph with known
blur filter ![]() .
To estimate the unblurred image
.
To estimate the unblurred image ![]() , we seek the
unconstrained minimum of
, we seek the
unconstrained minimum of
![]()
![]()
![]() ,
, ![]() and
and ![]() ,
a Jest linear-operator-with-adjoint to implement the convolution
,
a Jest linear-operator-with-adjoint to implement the convolution ![]() ,
and finally Jest's conjugate-gradient solver to estimate the solution
vector
,
and finally Jest's conjugate-gradient solver to estimate the solution
vector ![]() .
Figure 1 shows
the known filter,
the blurred input time series,
and the deconvolved result.
.
Figure 1 shows
the known filter,
the blurred input time series,
and the deconvolved result.
