




Next: Undrained joints, undrained matrix,
Up: Berryman & Wang: Double
Previous: STRESS-STRAIN FOR SINGLE POROSITY
pic
Figure 1
The double porosity model features a porous rock matrix
intersected by fractures. Three types of macroscopic pressure are pertinent
in such a model: external confining pressure pc, internal pressure
of the matrix pore fluid pf(1), and internal pressure of the fracture
pore fluid pf(2). A single porosity medium is one in which
either matrix or fracture porosity are present, but not both.

We now assume two distinct phases at the macroscopic level:
a porous matrix phase with the effective properties K(1), 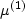 ,Km(1),
,Km(1), 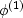 occupying volume fraction V(1)/V = v(1)
of the total volume and a macroscopic crack or joint phase occupying the
remaining fraction of the volume V(2)/V = v(2) = 1 - v(1). The key
feature distinguishing the two phases -- and therefore requiring this analysis
-- is the very high fluid permeability k(22) of the crack or joint phase
and the relatively lower permeability k(11) of the matrix phase. We could
also introduce a third independent permeability k(12) = k(21) for
fluid flow at the interface between the matrix and crack phases, but
for simplicity we assume here that this third permeability is essentially
the same as that of the matrix phase, so k(12) = k(11).
occupying volume fraction V(1)/V = v(1)
of the total volume and a macroscopic crack or joint phase occupying the
remaining fraction of the volume V(2)/V = v(2) = 1 - v(1). The key
feature distinguishing the two phases -- and therefore requiring this analysis
-- is the very high fluid permeability k(22) of the crack or joint phase
and the relatively lower permeability k(11) of the matrix phase. We could
also introduce a third independent permeability k(12) = k(21) for
fluid flow at the interface between the matrix and crack phases, but
for simplicity we assume here that this third permeability is essentially
the same as that of the matrix phase, so k(12) = k(11).
We have three distinct pressures: confining pressure 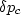 ,matrix-fluid pressure
,matrix-fluid pressure 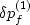 ,and joint-fluid pressure
,and joint-fluid pressure 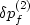 .Treating
.Treating 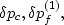 and
and 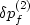 as the independent
variables in our double porosity theory, we define the dependent
variables
as the independent
variables in our double porosity theory, we define the dependent
variables 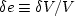 (as before),
(as before),
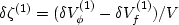 ,and
,and
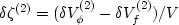 ,which are respectively the total volume dilatation, the
increment of fluid content in the matrix phase, and the increment of
fluid content in the joints. We assume that the fluid in the matrix
is the same kind of fluid as that in the cracks or joints, but that the two
fluid regions may be in different states of average stress and therefore need
to be distinguished by their respective superscripts.
,which are respectively the total volume dilatation, the
increment of fluid content in the matrix phase, and the increment of
fluid content in the joints. We assume that the fluid in the matrix
is the same kind of fluid as that in the cracks or joints, but that the two
fluid regions may be in different states of average stress and therefore need
to be distinguished by their respective superscripts.
Linear relations among strain, fluid content, and pressure then take the
general form
e - ^(1) - ^(2) =
a_11 & a_12 & a_13
a_21 & a_22 & a_23
a_31 & a_32 & a_33
- p_c - p_f^(1) - p_f^(2) .
By analogy with (all) and (allundrained), it is easy to see
that a12 = a21 and a13 = a31. The symmetry of the new
off-diagonal coefficients may be demonstrated by using Betti's reciprocal
theorem in the form
e & - ^(1) & - ^(2)
0 -p_f^(1) 0 =
e & -^(1) & -^(2) cr
0 0 -p_f^(2) ,
where unbarred quantities refer to one experiment and barred to
another experiment to show that
^(1)p_f^(1) =
a_23p_f^(2)p_f^(1) = a_32p_f^(1)p
_f^(2)
= ^(2)p_f^(2).
Hence, a23 = a32.
Similar arguments have often been used to establish the symmetry of the
other off-diagonal components. Thus, we have established that the matrix
in (generalstrainstress) is completely symmetric, so we need to determine
only six independent coefficients. To do so, we consider a series of
thought experiments,
including tests in both the short time and long time limits. The key idea
here is that at long times the two pore pressures must come to equilibrium
(pf(1) = pf(2) = pf as 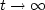 ) as long as the cross
permeability k(12) is finite. However, at very short times, we may assume
that the process of pressure equilibration has not yet begun, or equivalently
that k(12) = 0 at t = 0. We nevertheless assume that the pressure
in each of the two components have individually equilibrated on the average,
even at short times.
) as long as the cross
permeability k(12) is finite. However, at very short times, we may assume
that the process of pressure equilibration has not yet begun, or equivalently
that k(12) = 0 at t = 0. We nevertheless assume that the pressure
in each of the two components have individually equilibrated on the average,
even at short times.





Next: Undrained joints, undrained matrix,
Up: Berryman & Wang: Double
Previous: STRESS-STRAIN FOR SINGLE POROSITY
Stanford Exploration Project
8/21/1998
