




Next: SIMPLE EXAMPLE
Up: Rickett, et al.: STANFORD
Previous: INTRODUCTION
Assuming a v(z) earth with flat reflectors, we can define the
theoretical RMS velocities by
| 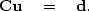 |
(71) |
where
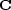
- is the matrix of causal integration, a lower triangular matrix of ones.
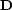
- is the matrix of causal differentiation, namely,
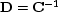 .
. 
- is a vector whose components range over the vertical
traveltime depth
 ,and whose component values contain the interval velocity squared
,and whose component values contain the interval velocity squared
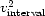 .
. 
- is a data vector whose components range over the vertical
travel time depth
 ,and whose component values contain the scaled RMS velocity squared
,and whose component values contain the scaled RMS velocity squared
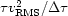 where
where
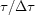 is the index on the time axis.
is the index on the time axis.
Start from a CMP gather q(t,i) moveout corrected with velocity v.
A good starting guess for our RMS velocity function
is the maximum ``instantaneous stack energy''
| 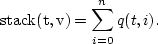 |
(72) |
An alternate starting guess for our RMS velocity function
is the conventional one of maximum semblance
| 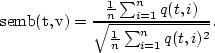 |
(73) |
In addition to the RMS velocities we
need a diagonal weighting matrix 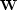 ,again found from stack energy or semblance,
that differentiates between RMS velocities which we have confidence in
(at reflectors) and ones that are more a function of noise in the data.
Our data fitting goal is to minimize the residual
,again found from stack energy or semblance,
that differentiates between RMS velocities which we have confidence in
(at reflectors) and ones that are more a function of noise in the data.
Our data fitting goal is to minimize the residual
| ![\begin{displaymath}
\bold 0
\quad\approx\quad
\bold W
\left[
\bold C\bold u
-
\bold d
\right] .\end{displaymath}](img250.gif) |
(74) |
Because we are multiplying our RMS function by  , we must
must make a slight change in our weighting function to give early
times approximately the same priority as later times.
, we must
must make a slight change in our weighting function to give early
times approximately the same priority as later times.
| 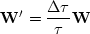 |
(75) |
To find the interval velocity
where there is no data (where the stack power theoretically vanishes)
we have the ``model damping'' goal to minimize
the wiggliness  of the squared interval velocity
of the squared interval velocity  where
where  equals
equals
| 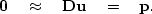 |
(76) |
To speed convergence we ``precondition'' these goals ()
by changing the optimization variable from
interval velocity squared
 to its wiggliness
to its wiggliness  .Substituting
.Substituting 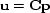 gives the two goals
expressed as a function of wiggliness
gives the two goals
expressed as a function of wiggliness  .
.
| ![\begin{eqnarray}
\bold 0
&\approx&
\bold W'
\left[
\bold C^2\bold p
-
\bold d
\right]
\\ \bold 0
&\approx&
\epsilon \bold p .\end{eqnarray}](img255.gif) |
(77) |
| (78) |





Next: SIMPLE EXAMPLE
Up: Rickett, et al.: STANFORD
Previous: INTRODUCTION
Stanford Exploration Project
7/5/1998
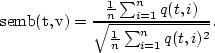
![]() to its wiggliness
to its wiggliness ![]() .Substituting
.Substituting ![]() gives the two goals
expressed as a function of wiggliness
gives the two goals
expressed as a function of wiggliness ![]() .
.