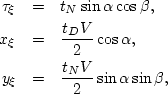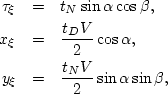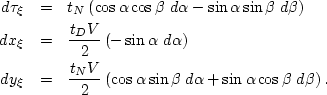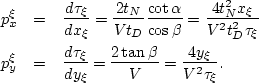Anti-aliasing constraints for 3-D prestack time migration

 For 3-D prestack time migration, the reflectors' dips $p^{{\rm \xi}}_x$ and $p^{{\rm \xi}}_y$, and the wavelet-stretch factor ${dt_{D}}/{d\tau_\xi}$,can be analytically derived as functions of the input and output trace geometry. Starting from the prestack time-migration ellipsoid, expressed as a parametric function of the angles $\alpha$ and $\beta$

$$\begin{eqnarray} \tau_\xi& = & t_{N}\sin \alpha\cos \beta, \nonumber \\ x_\xi& =... ...ha, \nonumber \\ y_\xi& = & \frac{t_{N}V}{2}\sin \alpha\sin \beta,\end{eqnarray}$$ (19)

where t_D is the time of the input impulse and t_N is the time after application of NMO. We differentiate the image coordinates with respect to the angles $\alpha$ and $\beta$;that is,

$$\begin{eqnarray} d\tau_\xi& = & t_{N}\left(\cos \alpha\cos \beta\;d\alpha- \sin ... ...s \alpha\sin \beta\;d\alpha+ \sin \alpha\cos \beta\;d\beta\right).\end{eqnarray}$$ (20)

We then eliminate the differentials $d\alpha$ and $d\beta$from this set of equations by setting respectively $dy_\xi$ equal to zero when evaluating the dip $p^{{\rm \xi}}_x$ in the in-line direction, and set $dx_\xi$ equal to zero when evaluating the dip in the cross-line direction $p^{{\rm \xi}}_y$.The second step is to eliminate the angles themselves and express the image dips as a function of the image coordinates $\left(\tau_\xi,x_\xi,y_\xi\right)$,

$$\begin{eqnarray} p^{{\rm \xi}}_x & = & \frac{d\tau_\xi}{dx_\xi} = \frac{2t_{N}}{... ...xi}{dy_\xi} = \frac{2\tan \beta}{V} = \frac{4y_\xi}{V^2\tau_\xi}. \end{eqnarray}$$ (21)

The wavelet-stretch factor can be easily derived by differentiating the summation surfaces of 3-D prestack time migration expressed as the hyperboloids  

$$t_{D}= t_s + t_g = \sqrt{\frac{\tau_\xi^2}{4} + \frac{\left\... ...{\left\vert{\bf \vec\xi_{xy}}-{\bf \vec g}\right\vert^2}{V^2}},$$ (22)

where ${\bf \vec s}$ and ${\bf \vec g}$ are the source and receiver coordinates vector, and ${\bf \vec\xi_{xy}}=\left(x_\xi,y_\xi\right)$ represents the horizontal components of the image coordinates vector. After a few simple algebra steps, we obtain

$$\frac{dt_{D}}{d\tau_\xi} = \frac{\tau_\xi}{4}\left(\frac{1}{t_s}+\frac{1}{t_g}\right).$$ (23)

 

 

Imaging under the edges of salt bodies: Analysis of an Elf North Sea dataset

Marie L. Prucha, Robert G. Clapp, and Biondo L. Biondi

marie@sep.Stanford.EDU, bob@sep.Stanford.EDU, biondo@sep.Stanford.EDU

ABSTRACT

Depth imaging techniques still face difficulties under the edges of salt bodies. Elf encountered such a problem in a 3-D survey in the North Sea where they hoped to image a reflector that lays beneath a salt body. Based on the 3-D data, Elf created 2-D synthetic model of the salt body and surrounding subsurface. By analyzing this synthetic model using Kirchoff depth migration and raytracing techniques, it became clear that the problem is largely due to poor illumination. The portion of the reflector under the edge of the salt dome only received illumination from a limited range of offsets. In addition to further analysis of both the synthetic and real datasets, investigations of possible solutions such as weighting appropriate offsets, inversion and/or the use of common reflection angle gathers seem warranted.