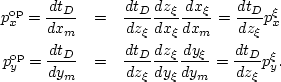Next: High-resolution imaging of salt
Up: Operator aliasing
Previous: Operator aliasing
The constraints on the data frequency
to avoid operator aliasing and image aliasing are different
in general;
and both sets of constraints must
be respected to assure a high-quality image.
However, the two sets of constraints
are equivalent in many practical situations.
The analysis is simple for zero-offset or constant-offset data,
where we can assume that the summation surfaces
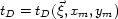 are only functions of the image point coordinates
are only functions of the image point coordinates 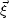 and of the midpoint coordinates of the data trace
and of the midpoint coordinates of the data trace 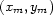 .
.
The first condition for linking
image aliasing to operator aliasing
is that the data are not spatially aliased,
and thus the operator anti-aliasing constraints
are the ones expressed in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ),
and not
the constraints expressed in equation (
),
and not
the constraints expressed in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
Comparing the constraints for operator anti-aliasing
[equation (
).
Comparing the constraints for operator anti-aliasing
[equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )]
with the constraints for image anti-aliasing
[equation (
)]
with the constraints for image anti-aliasing
[equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )]
we can easily notice that a necessary condition
for them being uniformly equivalent
is that the data sampling rates
)]
we can easily notice that a necessary condition
for them being uniformly equivalent
is that the data sampling rates
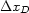 and
and 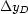 must be equal to the image sampling rates
must be equal to the image sampling rates
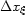 and
and 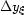 .The other necessary conditions are that
.The other necessary conditions are that
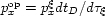 and
and
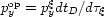 .These conditions are fulfilled in the
important case of spatially invariant imaging operators,
as it can be shown by
applying the chain rule to the derivative
of the summation surfaces tD
with respect to the midpoint coordinates of the data trace
.These conditions are fulfilled in the
important case of spatially invariant imaging operators,
as it can be shown by
applying the chain rule to the derivative
of the summation surfaces tD
with respect to the midpoint coordinates of the data trace
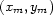 :
:
| 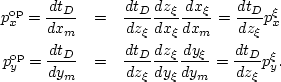 |
|
| (18) |
The equalities in (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
rely on the horizontal invariance of the imaging operator,
by requiring that the derivatives of the
horizontal coordinates of the image point with respect
to the horizontal coordinates of the data trace
to be equal to one.
For migration,
these conditions are strictly fulfilled only
in horizontally layered media,
though they are approximately fulfilled when migration
velocity varies smoothly.
Because equalities in (
)
rely on the horizontal invariance of the imaging operator,
by requiring that the derivatives of the
horizontal coordinates of the image point with respect
to the horizontal coordinates of the data trace
to be equal to one.
For migration,
these conditions are strictly fulfilled only
in horizontally layered media,
though they are approximately fulfilled when migration
velocity varies smoothly.
Because equalities in (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
do not require any other assumptions on the shape of the summation surfaces;
the same link between operator aliasing and image aliasing
exists for all spatially-invariant integral operators,
such as DMO and AMO.
)
do not require any other assumptions on the shape of the summation surfaces;
the same link between operator aliasing and image aliasing
exists for all spatially-invariant integral operators,
such as DMO and AMO.
The distinction between operator aliasing and image aliasing
can thus be safely ignored when time migrating well sampled
zero-offset data (, , ),
but it ought be respected when depth migrating irregularly
sampled prestack data.
This distinction is also important
when a priori assumptions
on the dips in the data permit setting
less stringent operator anti-aliasing constraints,
and thus the reflectors can be imaged with high-resolution
and without operator-aliasing artifacts.
An open, and more subtle, question
remains regarding the operator aliasing
of prestack data,
that in general do not constitute a minimal data set
().
However,
also in this case the constraints to avoid image aliasing
[equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )]
must be respected to produce high-quality and interpretable images.
)]
must be respected to produce high-quality and interpretable images.





Next: High-resolution imaging of salt
Up: Operator aliasing
Previous: Operator aliasing
Stanford Exploration Project
7/5/1998
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ),
and not
the constraints expressed in equation (
),
and not
the constraints expressed in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
Comparing the constraints for operator anti-aliasing
[equation (
).
Comparing the constraints for operator anti-aliasing
[equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )]
with the constraints for image anti-aliasing
[equation (
)]
with the constraints for image anti-aliasing
[equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )]
we can easily notice that a necessary condition
for them being uniformly equivalent
is that the data sampling rates
)]
we can easily notice that a necessary condition
for them being uniformly equivalent
is that the data sampling rates