




Next: Numerical results
Up: Rickett, et al.: STANFORD
Previous: Tetragonal eikonal equation
The fast-marching algorithm consists of two parts: minimum traveltime
selection and a local traveltime updating scheme. The selection
scheme is essentially based on Fermat's principle. The local traveltime
updating scheme can also be derived from the same principle using a
local linear interpolation, which provides the first-order accuracy.
triangle
Figure 6 A geometrical scheme for the traveltime updating procedure in two dimensions.
|
|  |
For simplicity, let us focus on the 2-D case
Consider a line segment with the end points A and B,
as shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . Let tA and tB denote the
traveltimes from a fixed distant source to points A and B,
respectively. Define a parameter
. Let tA and tB denote the
traveltimes from a fixed distant source to points A and B,
respectively. Define a parameter 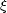 such that
such that 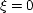 at A,
at A,
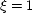 at B, and
at B, and 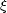 changes continuously on the line segment
between A and B. Then for each point of the segment, we can
approximate the traveltime by the linear interpolation formula
changes continuously on the line segment
between A and B. Then for each point of the segment, we can
approximate the traveltime by the linear interpolation formula
| 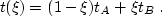 |
(157) |
Now let us consider an arbitrary point C in the vicinity of AB. If
we know that the ray from the source to C passes through some point
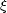 of the segment AB, then the total traveltime at C is
approximately
of the segment AB, then the total traveltime at C is
approximately
| 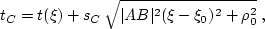 |
(158) |
where sC is the local slowness, 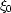 corresponds to the
projection of C to the line AB (normalized by the length |AB|),
and
corresponds to the
projection of C to the line AB (normalized by the length |AB|),
and 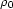 is the length of the normal from C to
is the length of the normal from C to 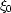 .Fermat's principle states that the actual ray to C corresponds to a
local minimum of the traveltime with respect to raypath perturbations.
According to our parameterization, it is sufficient to find a local
extreme of tC with respect to the parameter
.Fermat's principle states that the actual ray to C corresponds to a
local minimum of the traveltime with respect to raypath perturbations.
According to our parameterization, it is sufficient to find a local
extreme of tC with respect to the parameter 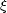 . Equating the
. Equating the
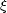 derivative to zero, we arrive at the equation
derivative to zero, we arrive at the equation
| 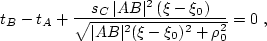 |
(159) |
which has (as a quadratic equation) the explicit solution for 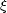 :
:
| 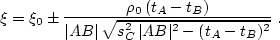 |
(160) |
Finally, substituting the value of 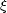 from (
from (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) into
equation (
) into
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and selecting the appropriate branch of the
square root, we obtain the formula
) and selecting the appropriate branch of the
square root, we obtain the formula
| 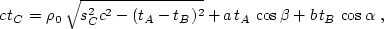 |
(161) |
where c = |AB|, a = |BC|, b = |AC|, angle  corresponds to
corresponds to 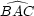 , and angle
, and angle 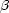 corresponds to
corresponds to
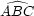 in the triangle ABC (Figure
in the triangle ABC (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
The above general procedure can be greatly simplified when applied to some
regular grids, such as the rectangular grid or the tetragonal grid.
This expression is even valid for unstructured grids.
As pointed out by Fomel ,
unstructured grids have some attractive computational advantages over the
regular ones. Moreover, the derivation provides a general principle,
which can be applied to derive analogous algorithms for other eikonal-type
(Hamilton-Jacobi) equations and their corresponding variational principles.
).
The above general procedure can be greatly simplified when applied to some
regular grids, such as the rectangular grid or the tetragonal grid.
This expression is even valid for unstructured grids.
As pointed out by Fomel ,
unstructured grids have some attractive computational advantages over the
regular ones. Moreover, the derivation provides a general principle,
which can be applied to derive analogous algorithms for other eikonal-type
(Hamilton-Jacobi) equations and their corresponding variational principles.





Next: Numerical results
Up: Rickett, et al.: STANFORD
Previous: Tetragonal eikonal equation
Stanford Exploration Project
7/5/1998


![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . Let tA and tB denote the
traveltimes from a fixed distant source to points A and B,
respectively. Define a parameter
. Let tA and tB denote the
traveltimes from a fixed distant source to points A and B,
respectively. Define a parameter ![]() such that
such that ![]() at A,
at A,
![]() at B, and
at B, and ![]() changes continuously on the line segment
between A and B. Then for each point of the segment, we can
approximate the traveltime by the linear interpolation formula
changes continuously on the line segment
between A and B. Then for each point of the segment, we can
approximate the traveltime by the linear interpolation formula
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) into
equation (
) into
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and selecting the appropriate branch of the
square root, we obtain the formula
) and selecting the appropriate branch of the
square root, we obtain the formula
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
The above general procedure can be greatly simplified when applied to some
regular grids, such as the rectangular grid or the tetragonal grid.
This expression is even valid for unstructured grids.
As pointed out by Fomel ,
unstructured grids have some attractive computational advantages over the
regular ones. Moreover, the derivation provides a general principle,
which can be applied to derive analogous algorithms for other eikonal-type
(Hamilton-Jacobi) equations and their corresponding variational principles.
).
The above general procedure can be greatly simplified when applied to some
regular grids, such as the rectangular grid or the tetragonal grid.
This expression is even valid for unstructured grids.
As pointed out by Fomel ,
unstructured grids have some attractive computational advantages over the
regular ones. Moreover, the derivation provides a general principle,
which can be applied to derive analogous algorithms for other eikonal-type
(Hamilton-Jacobi) equations and their corresponding variational principles.