Calculating the Regularization Parameter

It is the purpose of the regularization parameter, ${\epsilon}$, to weight the regularization residual so that the iterative solver does not focus on one goal while ignoring the other. For example, an ${\epsilon}$ that is too large will insure that the missing data is filled but it may be too smooth. On the other hand, an ${\epsilon}$ that is too small will not fill in much data and will tend to leave the acquisition footprint behind.

${\epsilon}$ is used in fitting goal (2) to balance the two goals. For now, I applied Jon Claerbout's idea . Within the conjugate solver routine, the gradient determines in which direction to minimize the residual.

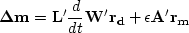$$\begin{eqnarray} \ {\bf \Delta m} = {\bf L'}\frac{d}{dt}{\bf W'r_d} + \epsilon {\bf A' r_m}\ \end{eqnarray}$$ (115)

Finding an ${\epsilon}$ which balances both goals we try:

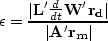$$\begin{eqnarray} \ \epsilon = \frac{\vert{\bf L'}\frac{d}{dt}{\bf W'r_d}\vert}{\vert{\bf A'r_m}\vert}\ \end{eqnarray}$$ (116)

In initial tests, I placed these equations in the solver and calculated a new ${\epsilon}$ for each iteration with the first ${\epsilon}$ value equal to 1. After about 15 iterations it converged to an almost constant value. This calculated ${\epsilon}$ was slightly lower than the ${\epsilon}$ that I found by trial and error. Figure was generated using an ${\epsilon}$ of 0.4 whereas the calculated ${\epsilon}$ for that figure, returned by the above equation, was approximately 0.3.

The calculated ${\epsilon}$ does not seem to work on the entire merged data set probably as a result of different data densities. The northern sparsely sampled region needs a different ${\epsilon}$ than the southern densely sampled region. In this case, a scalar ${\epsilon}$ value is not sufficient.