This method is strictly a vertical correction. It is naïve to assume that the misfit between the seismic horizon and the well logs is purely vertical, but well log measurements place no direct horizontal constraints on the output model. However, in the ``Future Work'' section I discuss how simple anisotropy can manifest itself in seismic data through vertical misfit, and how, through a simple inversion scheme, we may be able to quantify the degree of anisotropy.
We can directly measure the vertical discrepancy between ![]() and
and
![]() at the well locations, (xw,yw):
at the well locations, (xw,yw):
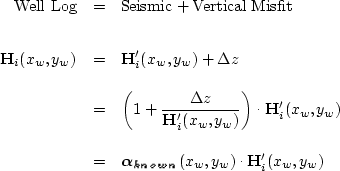 |
||
| (105) |
| |
(106) | |
| (107) |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
I choose the 2-D Laplacian,
).
I choose the 2-D Laplacian,
This problem is grossly underdetermined (![]() 15 known values vs. 1600
points in model space), so even for a good choice of
15 known values vs. 1600
points in model space), so even for a good choice of ![]() ,
convergence is slow - too slow, in fact, to make this method practical for
application to
real-world problems. To solve this problem, I use
preconditioning, defined as any change of variables which speeds convergence
of an iterative scheme.
,
convergence is slow - too slow, in fact, to make this method practical for
application to
real-world problems. To solve this problem, I use
preconditioning, defined as any change of variables which speeds convergence
of an iterative scheme.
In general, the preconditioning operator ![]() is defined by
is defined by
| |
(108) |
First wrap ![]() onto a helix, then unroll it to create a long 1-D filter,
as shown in Figure
onto a helix, then unroll it to create a long 1-D filter,
as shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
Through the process of spectral factorization, we compute a minimum phase
filter
.
Through the process of spectral factorization, we compute a minimum phase
filter ![]() whose autocorrelation is
whose autocorrelation is ![]() :
:
![]() .
Since
.
Since ![]() is minimum phase, successive convolution with
is minimum phase, successive convolution with ![]() and
and
![]() is
multiplication with lower and upper diagonal matrices, respectively.
Therefore, the inverse operation, deconvolution, is matrix inversion:
is
multiplication with lower and upper diagonal matrices, respectively.
Therefore, the inverse operation, deconvolution, is matrix inversion:
![]() ,
which can be done very quickly in this case with simple backsubstitution,
an
,
which can be done very quickly in this case with simple backsubstitution,
an ![]() operation! For more
details on the spectral factorization methods used at SEP, see
(), or more recently, ().
operation! For more
details on the spectral factorization methods used at SEP, see
(), or more recently, ().
 |
Now that we can compute the preconditioner ![]() with confidence,
repose the original problem. First apply the following change of variables:
with confidence,
repose the original problem. First apply the following change of variables:
| |
(109) |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) into Equations (
) into Equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and
(
) and
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) to obtain
) to obtain
| |
||
| (110) |
We solve for ![]() iteratively, then convert back to
iteratively, then convert back to ![]() via equation
via equation
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . Figure
. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the resultant
shows the resultant
![]() (x,y)
for both the shallow and deep horizons. Does preconditioning work? Yes!
In this example, the rate of convergence is increased by two orders of magnitude
by preconditioning, e.g., roughly 1000 versus 10 CD iterations.
(x,y)
for both the shallow and deep horizons. Does preconditioning work? Yes!
In this example, the rate of convergence is increased by two orders of magnitude
by preconditioning, e.g., roughly 1000 versus 10 CD iterations.
 |
Now we compute the final output model, ![]()
| |
(111) |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , respectively.
, respectively.
 |
 |