




Next: Example
Up: Rickett, et al.: STANFORD
Previous: TIME- AND SPACE-VARYING PEFS
We estimate missing data in two steps of linear least squares ().
The first step is estimation of PEFs.
After the PEFs have been estimated they are used to fill in the empty trace bins.
This is the second step of least squares.
We want the recorded and estimated data to have the same dips.
Since the dip information is now carried in the PEFs,
this is once again specifying that the convolution of the filter and data
should give the minimum output, except that now the filters are known and the
data is unknown.
We constrain the data by specifying that the originally recorded data cannot change.
To separate the known and unknown data we have a known data selector 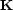 and an
unknown data selector
and an
unknown data selector 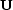 , with
, with 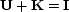 .
These multiply by 1 or depending on whether the data was originally recorded or not.
With
.
These multiply by 1 or depending on whether the data was originally recorded or not.
With 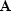 signaling convolution with the PEF and
signaling convolution with the PEF and 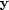 the vector of data, the regression is
the vector of data, the regression is 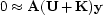 , or
, or 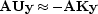 .
.
While a complete set of PEFs works well for destroying the data, I have found that it is not the best choice for reconstructing it; interpolation with PEFs estimated at every data point gives poor results.
Probably that just means I have not found the right value of  in (
in (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), or that I have not found the right roughener.
At any rate, it is easy to just reduce the number of filters slightly, from every data point to perhaps every fifth.
This is similar to putting an extra roughener in the damping equation, in that it is essentially an infinite penalty on variations of
), or that I have not found the right roughener.
At any rate, it is easy to just reduce the number of filters slightly, from every data point to perhaps every fifth.
This is similar to putting an extra roughener in the damping equation, in that it is essentially an infinite penalty on variations of  between small groups of samples, and it has the important economizing effect of reducing the memory allocation.
A full set of
between small groups of samples, and it has the important economizing effect of reducing the memory allocation.
A full set of 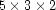 PEFs is like allocating an extra 22 copies of the data in memory, a slightly subsampled set is only a few extra copies.
This is a similar to using very small patches.
In the method where the patches are independent (), the number of filter coefficients puts a lower bound on patch size; the problem has to stay well overdetermined to produce a useful PEF.
Using smoothly nonstationary filters effectively reduces the minimum patch size, so that the filter estimation problem can be underdetermined.
PEFs is like allocating an extra 22 copies of the data in memory, a slightly subsampled set is only a few extra copies.
This is a similar to using very small patches.
In the method where the patches are independent (), the number of filter coefficients puts a lower bound on patch size; the problem has to stay well overdetermined to produce a useful PEF.
Using smoothly nonstationary filters effectively reduces the minimum patch size, so that the filter estimation problem can be underdetermined.
Figure coeffs illustrates the filter subsampling with a simple synthetic.
A random 1-D sequence, uniformly shifted along the horizontal axis, is used to estimate a set of PEFs.
A single PEF can predict this panel perfectly with a -1 value in the correct place.
The right side of the figure graphs the individual filter coefficient that should be equal to -1, with the horizontal axis tracking different PEFs.
Predictably, when the PEFs are estimated at every point (the upper graph), the values have noticeably greater variance and decreased energy than when the PEFs are estimated at every fifth point (the lower graph).
Not shown, the coefficients at other lags in the upper case have more variance and more energy than in the lower case.
They upper values still destroy the data perfectly, but they cannot reconstruct it.
coeffs
Figure 1 Effect of slightly subsampling the filter estimation. The left shows a very predictable synthetic. The right shows two sets of coefficients that should be equal to -1. The upper graph is the coefficients estimated at every data sample, the lower graph shows the coefficients obtained when PEFs are only estimated at every fifth data point.










Next: Example
Up: Rickett, et al.: STANFORD
Previous: TIME- AND SPACE-VARYING PEFS
Stanford Exploration Project
7/5/1998
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), or that I have not found the right roughener.
At any rate, it is easy to just reduce the number of filters slightly, from every data point to perhaps every fifth.
This is similar to putting an extra roughener in the damping equation, in that it is essentially an infinite penalty on variations of
), or that I have not found the right roughener.
At any rate, it is easy to just reduce the number of filters slightly, from every data point to perhaps every fifth.
This is similar to putting an extra roughener in the damping equation, in that it is essentially an infinite penalty on variations of 