




Next: Conclusions
Up: Rickett, et al.: STANFORD
Previous: Suppressing wraparound artifacts of
For an alternative spectral approach, I adopted the Chebyshev- method (, ). The Chebyshev-
method (, ). The Chebyshev- velocity continuation
algorithm consists of the following steps:
velocity continuation
algorithm consists of the following steps:
- 1.
- Transform the regular grid in t to Gauss-Lobato collocation
points, required for the fast Chebyshev transform. First, a new
variable
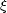 is introduced by the shift transform:
is introduced by the shift transform:
| 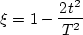 |
(91) |
so that the domain 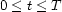 is mapped into the domain
is mapped into the domain 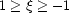 . Second, the
. Second, the 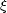 grid points are distributed
regularly in the cosine projection:
grid points are distributed
regularly in the cosine projection: 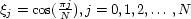 .
. - 2.
- Transform the initial image P0 (x,t) into the Chebyshev space
in
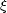 and Fourier transform in x, using the FFT algorithm. The
Chebyshev-Fourier representation of P0 (x,t) is
and Fourier transform in x, using the FFT algorithm. The
Chebyshev-Fourier representation of P0 (x,t) is
| 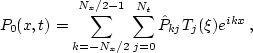 |
(92) |
where Tj denotes the Chebyshev polynomial of degree j.
- 3.
- Apply equation (
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) to advance the image in velocity v.
It is convenient to rewrite this equation in the form
) to advance the image in velocity v.
It is convenient to rewrite this equation in the form
| 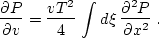 |
(93) |
In the Chebyshev- domain, the double differentiation in x is
performed by multiplying the Fourier transform of P by -k2, and
integration in
domain, the double differentiation in x is
performed by multiplying the Fourier transform of P by -k2, and
integration in 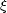 is performed
as a direct operations on the Chebyshev coefficients. In
particular, if
is performed
as a direct operations on the Chebyshev coefficients. In
particular, if 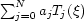 is the Chebyshev
representation of the function
is the Chebyshev
representation of the function 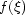 , then the coefficients
bj of
, then the coefficients
bj of 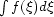 are defined by the relation
are defined by the relation
| 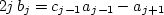 |
(94) |
where c0 = 2, cj = 0 for j < 0, and cj = 1 for j > 0.
The constant of integration (and, correspondingly, the coefficient
b0) can be found at each velocity step from the boundary
conditions (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), which are transformed to the form
), which are transformed to the form
| 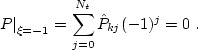 |
(95) |
For the velocity advancement I used an implicit Crank-Nicolson scheme,
which is unconditionally stable independent of the velocity step size.
By writing equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) in the matrix form
) in the matrix form
| 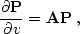 |
(96) |
the Crank-Nicolson advancement is represented by the equation
| 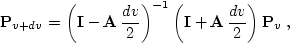 |
(97) |
where 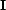 is the identity matrix. The inverted matrix
is the identity matrix. The inverted matrix
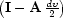 has a tridiagonal
structure, except for the first row, implied by the boundary
condition (
has a tridiagonal
structure, except for the first row, implied by the boundary
condition (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). A careful treatment of the boundary
condition by the matrix-bordering method (, ) allows
for an efficient inversion at a tridiagonal solver speed.
). A careful treatment of the boundary
condition by the matrix-bordering method (, ) allows
for an efficient inversion at a tridiagonal solver speed.
- 4.
- Transform the result of the velocity advancement back to the
physical domain.
- 5.
- Transform the grid back to being regularly space in t.
cheb1
Figure 6 Synthetic seismic data before (left) and
after (right) transformation to the Chebyshev grid in squared time.





cheb1-inv
Figure 7 The left plots show the reconstruction of the original data
after transforming back from the Chebyshev grid to the original t
grid. The right plots show the difference with the original model.
Top: using the original grid size (Nt = 200). Bottom: increasing
the grid size by a factor of three.





The first advantage of the Chebyshev approach comes from the better
conditioning of the grid transform. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the
synthetic data before and after the grid transform. Figure
shows the
synthetic data before and after the grid transform. Figure
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a reconstruction of the original data after
transforming back from the Chebyshev grid (Gauss-Lobato collocation
points). The difference with the original image is negligibly small.
shows a reconstruction of the original data after
transforming back from the Chebyshev grid (Gauss-Lobato collocation
points). The difference with the original image is negligibly small.
cheb1-fft
Figure 8 Left: Synthetic data after Chebyshev
transform. Right: the real part of the Fourier transform in the
space coordinate.





The second advantage is the compactness of the Chebyshev
representation. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the data after the
decomposition into Chebyshev polynomials in
shows the data after the
decomposition into Chebyshev polynomials in 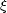 and Fourier
transform in x. We observe a very rapid convergence of the Chebyshev
representation: a relatively small number of polynomials suffices to
represent the data.
and Fourier
transform in x. We observe a very rapid convergence of the Chebyshev
representation: a relatively small number of polynomials suffices to
represent the data.
cheb-impl
Figure 9 Impulse responses (Green's functions) of
velocity continuation, computed by the Chebyshev- method. Top:
without zero padding, bottom: with zero padding on the x axis. The
left plots correspond to continuation to a larger velocity (+1
km/sec); the right plots, smaller velocity, (-1 km/sec).
method. Top:
without zero padding, bottom: with zero padding on the x axis. The
left plots correspond to continuation to a larger velocity (+1
km/sec); the right plots, smaller velocity, (-1 km/sec).





The third advantage is the proper handling of the non-periodic boundary
conditions. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the velocity continuation
impulse responses, computed by the Chebyshev method. As expected, no
wraparound artifacts occur on the time axis, and the accuracy of the
result is noticeably higher than in the case of finite differences
(Figure
shows the velocity continuation
impulse responses, computed by the Chebyshev method. As expected, no
wraparound artifacts occur on the time axis, and the accuracy of the
result is noticeably higher than in the case of finite differences
(Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).





Next: Conclusions
Up: Rickett, et al.: STANFORD
Previous: Suppressing wraparound artifacts of
Stanford Exploration Project
7/5/1998
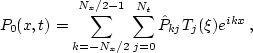
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) to advance the image in velocity v.
It is convenient to rewrite this equation in the form
) to advance the image in velocity v.
It is convenient to rewrite this equation in the form
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), which are transformed to the form
), which are transformed to the form
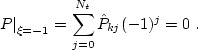
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) in the matrix form
) in the matrix form
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). A careful treatment of the boundary
condition by the matrix-bordering method (, ) allows
for an efficient inversion at a tridiagonal solver speed.
). A careful treatment of the boundary
condition by the matrix-bordering method (, ) allows
for an efficient inversion at a tridiagonal solver speed.



