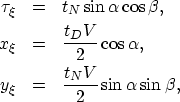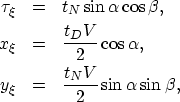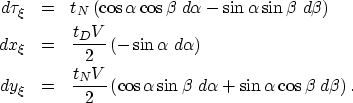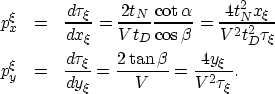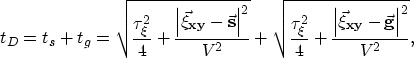Next: About this document ...
Up: Biondi: Kirchhoff imaging beyond
Previous: REFERENCES
For 3-D prestack time migration,
the reflectors' dips
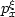 and
and 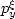 ,
and the wavelet-stretch factor
,
and the wavelet-stretch factor 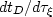 ,can be analytically derived
as functions of the input and output trace geometry.
Starting from the prestack time-migration ellipsoid,
expressed as a parametric function of the angles
,can be analytically derived
as functions of the input and output trace geometry.
Starting from the prestack time-migration ellipsoid,
expressed as a parametric function of the angles  and
and 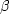
| 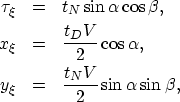 |
|
| |
| (7) |
where tD is the time of the input impulse
and tN is the time after application of NMO.
We differentiate the image coordinates
with respect to the angles  and
and 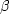 ;that is,
;that is,
| 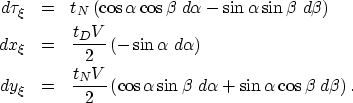 |
|
| |
| (8) |
We then eliminate the differentials 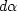 and
and 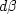 from this set of equations
by setting respectively
from this set of equations
by setting respectively 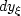 equal to zero when evaluating the
dip
equal to zero when evaluating the
dip 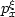 in the in-line direction,
and set
in the in-line direction,
and set 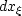 equal to zero when evaluating the dip in the cross-line
direction
equal to zero when evaluating the dip in the cross-line
direction 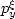 .The second step is to eliminate the angles themselves
and express the image dips
as a function of the image coordinates
.The second step is to eliminate the angles themselves
and express the image dips
as a function of the image coordinates
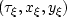 ,
,
| 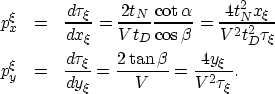 |
|
| (9) |
The wavelet-stretch factor can be easily derived
by differentiating the summation surfaces of 3-D prestack time migration
expressed as the hyperboloids
| 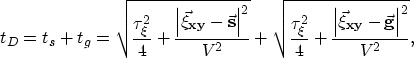 |
(10) |
where 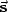 and
and 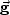 are the source and receiver coordinates vector,
and
are the source and receiver coordinates vector,
and 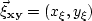 represents the horizontal components
of the image coordinates vector.
After a few simple algebra steps, we obtain
represents the horizontal components
of the image coordinates vector.
After a few simple algebra steps, we obtain
| 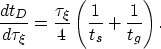 |
(11) |





Next: About this document ...
Up: Biondi: Kirchhoff imaging beyond
Previous: REFERENCES
Stanford Exploration Project
7/5/1998