Next: The Marmousi model
Up: Alkhalifah & Fomel: Fast
Previous: fast marching in spherical
Most of the numerical examples shown below
are to demonstrate the advantages of using the spherical, or polar, coordinate
system, over the Cartesian one, with this new efficient and unconditionally stable eikonal solver. The
Cartesian coordinate implementation includes analytically solving for the first layer of grid
points around the point source to reduce the wavefront curvature errors.
At the top of Figure 6, we show
the traveltime in a homogeneous medium computed using a second-order in time, or first order in ray parameter,
eikonal solver
van Trier and Symes (1991), as well as using the grid adaptive scheme to achieve better stability (The code
was built by Dave Hale, 1991).
This eikonal solver, because of its higher-order accuracy, serves as the reference for testing
the accuracy of the fast marching implementation in different coordinate systems. In addition, this particular
second-order solver
is exact in
homogeneous media, because it is executed in polar coordinates.
At the bottom of Figure 6, we show the traveltime difference,
or error, between implementing the fast-marching method in
Cartesian coordinates (left), polar coordinates (right), in contrast to the more accurate second-order scheme.
As expected, the majority of the errors
in the Cartesian coordinate implementation are concentrated around the 45-degree angle wave propagation.
The errors also increase more rapidly near the source where the wavefront curvature is the largest.
The polar coordinate implementation, on the other hand, is almost exact for homogeneous media. In
this case, the waves
propagate in a plane wave geometry with respect to the grid orientation.
wkbjvh
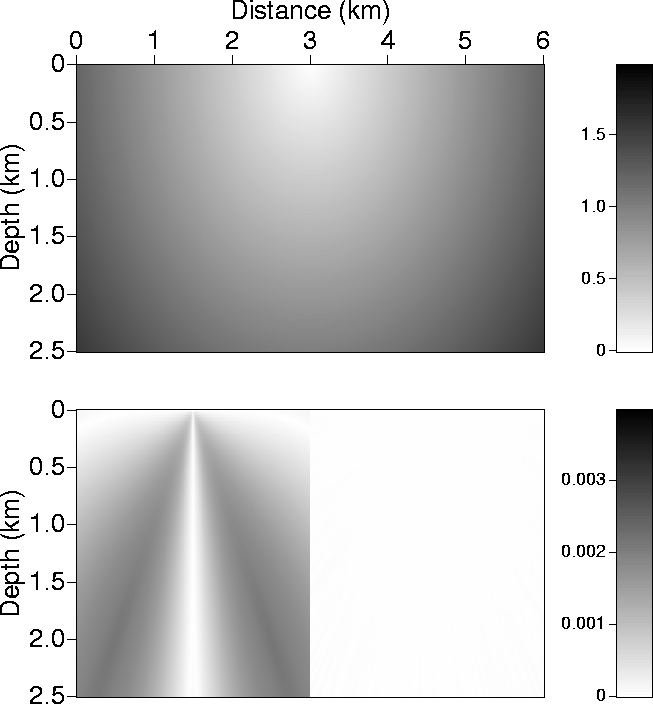
Figure 6 The top section shows
traveltimes (in seconds) in a homogeneous medium with velocity equal
to 2500 m/s, resulting from a source located at the surface at distance 3000 m. The bottom section shows the
absolute difference, or errors, in seconds between traveltimes calculated by
the fast marching method using the Cartesian coordinates (left) and the
polar coordinates (right) in comparison to the more accurate second-order eikonal solver. In this
homogeneous case, the polar
coordinate fast marching method has practically no errors.

Figure 7 shows traveltimes in a slightly more complicated velocity model. The
traveltime contours computed using the various methods practically coincide.
vtcont-simpleg
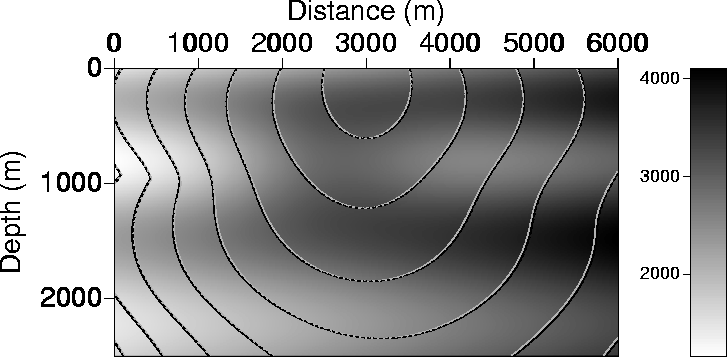
Figure 7 Contours of traveltimes resulting from a source placed on the surface
at a distance of 3000 m. The traveltime contours are
superimposed on the velocity model (in m/s).
The solid black curves correspond to the solution of the more accurate second-order eikonal solver. The gray
curves correspond to use of the fast marching
eikonal solver in Cartesian coordinates; the dashed curves,
in polar coordinates. The three curves are really close.

A closer look, in Figure 8, reveals, as in Figure 6,
the details of the errors using the different coordinate schemes.
The result of using the second-order eikonal solver is shown at the top,
and the absolute traveltime errors
from using the fast marching method in
Cartesian coordinates (left), and polar coordinates (right) are shown at the bottom. The Cartesian and
polar coordinate implementations have about the same computational cost; both are far faster than the
more accurate second-order
scheme. Clearly, the polar coordinate implementation has far fewer
errors than the Cartesian coordinate one.
wkbjvxz
Figure 8 The top section shows the traveltimes, in seconds, for waves propagating
in the model shown in Figure 7, resulting from a source located at
the surface at a distance of 3000 m. The bottom sections show the
absolute difference, or errors, in seconds between traveltime calculated by
the fast marching method using the Cartesian coordinates (left) and the
polar coordinates (right) in comparison to the more accurate second-order eikonal solver.






Next: The Marmousi model
Up: Alkhalifah & Fomel: Fast
Previous: fast marching in spherical
Stanford Exploration Project
10/9/1997