Incremental DELAUNAY TRIANGULATION and related problems

Delaunay triangulation Delaunay (1934); Guibas and Stolfi (1985); Sibson (1978) is a fundamental geometric construction, which has numerous applications in different computational problems. For a given set of nodes (points on the plane), Delaunay triangulation constructs a triangle tessellation of the plane with the initial nodes as vertices. Among all possible triangulations, the Delaunay triangulation possesses optimal properties, which make it very attractive for practical applications, such as computational mesh generation. One of the most well-known properties is maximizing the minimum triangulation angle. In three dimensions, Delaunay triangulation generalizes naturally to a tetrahedron tessellation.

Several optimal-time algorithms of Delaunay triangulation (and its counterpart-Voronoi diagram) have been proposed in the literature. The divide-and-conquer algorithm Guibas and Stolfi (1985); Shamos and Hoey (1975) and the sweep-line algorithm Fortune (1987) both achieve the optimal $O (N \log N)$ worst-case time complexity. Alternatively, a family of incremental algorithms has been used in practice because of their simplicity and robustness. Though the incremental algorithm can take O (N²) time in the worst case, the expectation time can still be $O (N \log N)$, provided that the nodes are inserted in a random order Guibas et al. (1992).

The incremental algorithm consists of two main parts:

1.

Locate a triangle (or an edge), containing the inserted point.

2.

Insert the point into the current triangulation, making the necessary adjustments.

The Delaunay criterion can be reduced in the second step to a simple InCircle test Guibas and Stolfi (1985): if a circumcircle of a triangle contains another triangulation vertex in its circumcenter, then the edge between those two triangles should be ``flipped'' so that two new triangles are produced. The testing is done in a recursive fashion consistent with the incremental nature of the algorithm. When a new node is inserted inside a triangle, three new triangles are created, and three edges need to be tested. When the node falls on an edge, four triangles are created, and four edges are tested. In the case of test failure, a pair of triangles is replaced by the flip operation with another pair, producing two more edges to test. Under the randomization assumption, the expected total time of point insertion is O (N). Randomization can be considered as an external part of the algorithm, provided by preprocessing.

Guibas et al. (1992) reduce the point location step to an efficient $O (N \log N)$ procedure by maintaining a hierarchical tree structure: all triangles, occurring in the incremental triangulation process, are kept in memory, associated with their ``parents.'' One or two point location tests (CCW tests) are sufficient to move to a lower level of the tree. The search terminates with a current Delaunay triangle.

To test the algorithmic performance of the incremental construction, I have profiled the execution time of my incremental triangulation program with the Unix pixie utility. The profiling result, shown in Figures 6 and 7, complies remarkably with the theory: $O (N \log N)$ operations for the point location step, and O (N) operations for the point insertion step. The experimental constant for the insertion step time is about 8.6. The experimental constant for the point location step is 4. The CPU time, depicted in Figure 8, also shows the expected $O (N \log N)$ behavior.

 

itime Figure 6 The number of point insertion operations (InCircle test) plotted against the number of points.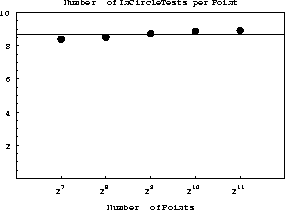

 

ctime Figure 7 Number of point location operations (CCW test) plotted against the number of points.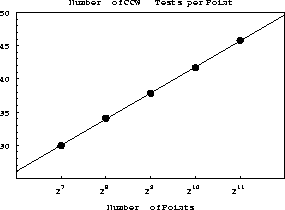

 

time Figure 8 CPU time (in seconds per point) plotted against the number of points.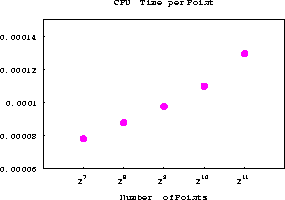

A straightforward implementation of Delaunay triangulation would provide an optimal triangulation for any given set of nodes. However, the quality of the result for unfortunate geometrical distributions of the nodes can be unsatisfactory. In the rest of this appendix, I describe three problems, aimed at improving the triangulation quality: conforming triangulation, triangulation of height fields, and mesh refinement. Each of these problems can be solved with a variation of the incremental algorithm.