Boundary values

As mentioned in the preceding section, the application of formulas (11-12) requires the existence of known boundary values for both the first value of $\tau$ (next to the wave source) and the extreme values of the take-off angle $\gamma$. Therefore, we have to initialize the complete first wavefront as well as two boundary rays that represent all the extreme points of each consequent wavefront (that is, for the first and last considered take-off angle).

To initialize the points on the first wavefront, we consider that the velocity is constant around the source, and therefore this wavefront becomes a circle centered at the source. This is a reasonable assumption because we use a finite difference scheme with very small time steps, and the velocity models have limited local variation.

The values of the boundary rays are externally supplied. This apparent problem is very easy to solve by using a ray tracing program to compute the trajectories of these two boundary rays. We can shoot several ``trial'' rays and select the ones that are the smoothest and that penetrate the most into the model.

 

solution Figure 3 The double solution of the system of equations (7-10). D and E are the intersection points between the circle given by equation (7) and the line given by equation (10). Point O is the previous point on the ray going through B. The distance (OE) is smaller than the distance (OD) and, therefore, D is the next selected point. The middle ray is defined locally by the succession of points (-O-B-D-).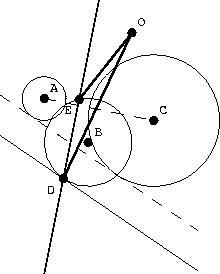