Triangulation

There are at least two methods we can use to obtain the optimal triangulation. One option is to build a set of triangles (which, of course, do not intersect) and then to apply an iterative process aimed to improve the previous triangulation to the constrained Delaunay one. The second option is to use an incremental algorithm in which to build the desired Delaunay triangulation in a iterative way, step by step.

We have selected the latter option because it is the fastest and the implementation is fairly easy. The algorithm we use is to

1.

Iteratively select a group of two rays (in the 2-D case) or three rays (in the 3-D case) according to the take-off angle(s) so that the entire data space is eventually covered.

2.

Select two doublets of points (in the 2-D case) or triplets of points (in the 3-D case) on the considered rays. They act like a base with two (in 2-D) or three (in 3-D) ``candidate' points.

3.

Analyze all the candidates to see which best fits the Delaunay criterion. This procedure translates into performing an in-circle test (in 2-D) or an in-sphere test (in 3-D) O'Rourke (1993).

4.

Advance the base with the point selected at the proceeding item, and proceed to the next step by selecting a new group of candidate points. Of course, only one will be different from the proceeding group of candidates.

 

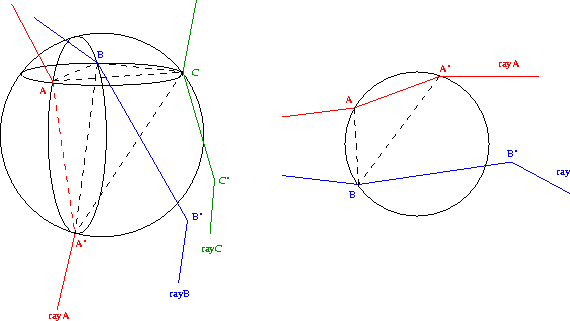
circle-sphere
Figure 2 Right: the 2-D case. A and B are the base points; A' and B' are the candidate points. B' falls outside the circle built on ABA'; therefore BA' is the next base. Left: the 3-D case. A, B, and, C are the base points; A', B', and C' are the candidate points. B' and C' fall outside the sphere built on ABCA'; therefore ACA' is the next base.

A difficult situation appears when the candidate points are not on the same side of the advancing base. In such cases, it is no longer possible to apply only the Delaunay criterion. Other rules are needed to get the correct new base. Our choice is to advance the points on the ray that restore fastest all the candidate points on the same side of the base. We do so by saving the ray of the last advance and performing the new advance on one of the other rays.