




Next: The cross-product filter
Up: Problem formulation
Previous: Problem formulation
The linear inverse problem we solve for each frequency component
can be written as a matrix
equation:
| 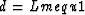 |
(1) |
where the vector d represents the irregular input data, L represents
the modeling operator, and m stands for the regularly sampled model.
The least-squares solution to equation equ1 can be expressed, for the
overdetermined case, as:
| 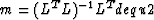 |
(2) |
and, for the underdetermined case, as
| 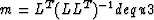 |
(3) |
These solutions define a least-squares inverse or pseudo-inverse to the
operator L. From equation equ2, we write this inverse
in terms of L
and its adjoint LT as
| 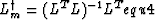 |
(4) |
whereas in equ3 the inverse for the underdetermined problem is
| 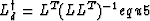 |
(5) |
Applying the pseudo-inverse of equ4 is equivalent to applying the
adjoint operator LT, followed by a spatial filtering of the model
space by the inverse of LTL. Therefore, we refer to this
inverse as model-space inverse.
In equation equ5 the adjoint operator is applied after the data have been
filtered with the inverse of LLT and, consequently,
we refer to this inverse as
data-space inverse.
To compute any of these two inverses, the problem reduces to estimating
an inverse for the cross-product matrix LTL, alternatively, (LLT).





Next: The cross-product filter
Up: Problem formulation
Previous: Problem formulation
Stanford Exploration Project
10/9/1997