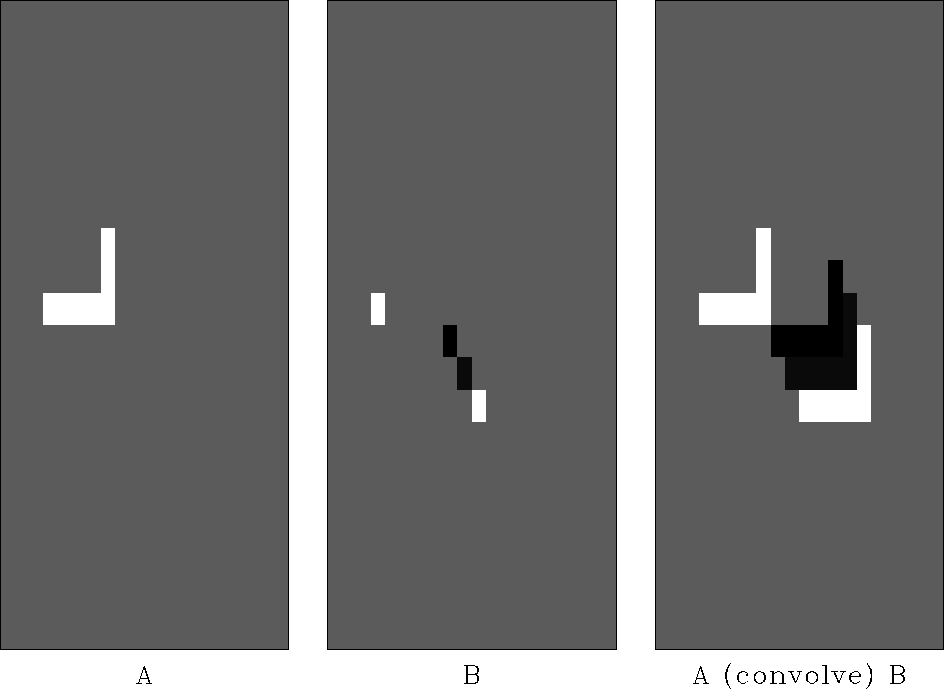
 |
Figure 1 Two-dimensional convolution (as performed in one dimension).
 |
First we must map two dimensions into one. Wind a rope around your arm into a helical coil that neatly covers your arm. This coil is a two-dimensional surface while the rope is one-dimensional. Now paint a seismic signal on one of the loops around your arm, and likewise paint all the loops with other signals so you have a seismic section on your arm. It is OK if the backside of your arm has no paint on it; we'll call that zero padding.
Seismologists sometimes use the word ``supertrace'' to describe a collection of seismograms stored ``end-to-end''. Fortran programmers will recognize that Fortran's way of storing 2-D arrays in one-dimensional memory is exactly what we need for this helical mapping. Likewise, in 3-D we simply append one plane after another (like a 3-D Fortran array). It is easier to code than to explain or visualize a spool or torus wrapped with string, etc.
A basic idea of filtering, be it in one dimension, two dimensions, or more, is that you have some filter coefficients and some sampled data; you pass the filter over the data; at each location you find an output by crossmultiplying the filter coefficients times the underlying data and summing the terms. The order in which you produce the outputs is irrelevant. You could compute the results in parallel. Figure 2 shows a filter and some data organized on a helical coil. Since the output values can be computed in any order, we can slide the filter coil over the data coil in any direction. We could, however, slide the filter over the data in the screwing order that a nut passes over a bolt. The screw order is the same order that would be used if we were to unwind the coils into one-dimensional strips and convolve them across one another. The same filter coefficients overlay the same data values if the 2-D coils are unwound into 1-D strips. The helix idea allows us to obtain the same convolution output in either of two ways, a one-dimensional way, or a two-dimensional way. I used the one-dimensional way to compute the obviously two-dimensional result in Figure 1.
|
coil
Figure 2 Filtering on a helix. The same filter coefficients overlay the same data values if the 2-D coils are unwound into 1-D strips. | 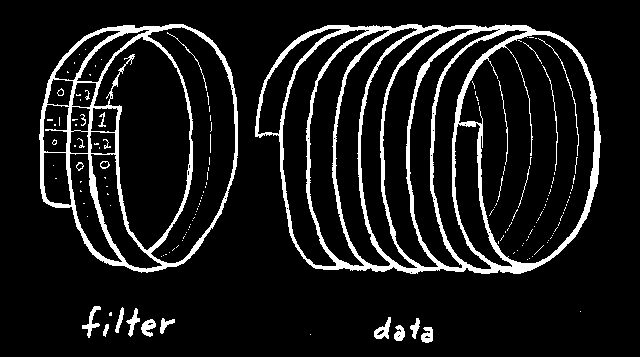 |
Deconvolution (polynomial division) can undo convolution (polynomial multiplication). A magical property of the helix is that we can consider 1-D convolution to be the same as 2-D convolution. Hence is a second magical property: We can use 1-D deconvolution to undo convolution, whether that convolution was 1-D or 2-D. Thus, we have discovered how to undo 2-D convolution. We have discovered that 2-D deconvolution on a helix is equivalent to 1-D deconvolution. We have learned how to do multidimensional deconvolution.
Deconvolution is recursive filtering. Recursive filter outputs cannot be computed in parallel, but must be computed sequentially as in one dimension, namely, in the order that the nut screws on the bolt.
Recursive filtering sometimes solves big problems with astonishing speed. It can propagate energy rapidly for long distances. Unfortunately, recursive filtering can also be unstable. There is a large literature and extensive technology about recursive filtering in one dimension. The helix allows us to apply that technology to two (and more) dimensions. It is a huge technological breakthrough.