 |
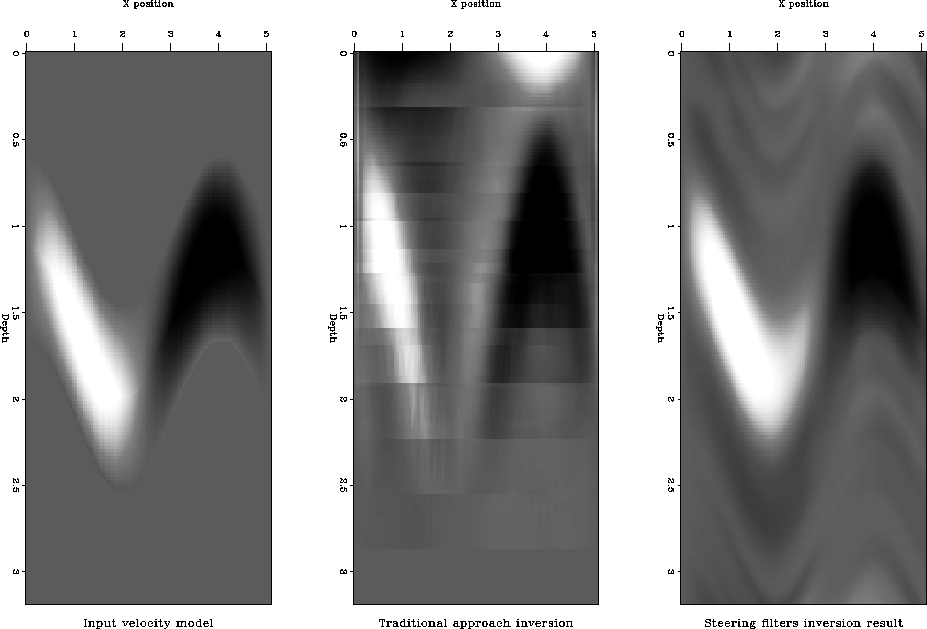
Figure 10 Left, slowness perturbation model; center, inversion result using Laplacian smoother; right, inversion result using steering filters.
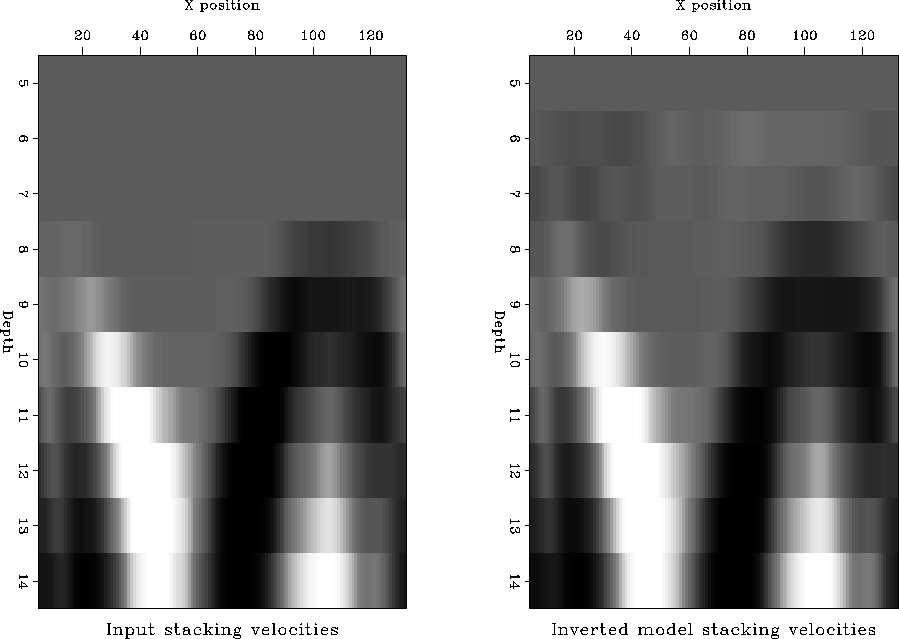
We constructed a synthetic interval slowness perturbation model (Figure toldi-steer, left panel) where the perturbations from zero follow a sinusoidal path, and the anomalies go from positive to negative as you go from left to right. We used Toldi's forward operator to compute stacking velocities at various depth levels (Figure toldi-stack, left panel), in this case we simulating collecting stacking velocity at 10 evenly spaced depths (compared to 160 depth locations in our interval slowness model), assuming a cable length of 2 km.
 |
 |
We applied a fairly traditional inversion methodology to estimate our interval velocity perturbations:
![]()
Where ![]() , is the Toldi operator;
, is the Toldi operator; ![]() , is a Laplacian smoother;
, is a Laplacian smoother;
![]() , is our interval slowness perturbation model; and
, is our interval slowness perturbation model; and ![]() , is
our data, stacking slowness perturbations.
, is
our data, stacking slowness perturbations.
The center panel of Figure toldi-steer shows the inversion result.
We tried a variety of ![]() values, selecting one that
created a rough
model, but did a fairly good job recovering the correct interval velocity
perturbations.
Next, we attempted to recover the interval slowness perturbations, starting
from the same stacking slowness perturbations, using the
steering filter
methodology.
We constructed our steering filters to follow the sinusoidal pattern of the
model and changed our fitting goal to:
values, selecting one that
created a rough
model, but did a fairly good job recovering the correct interval velocity
perturbations.
Next, we attempted to recover the interval slowness perturbations, starting
from the same stacking slowness perturbations, using the
steering filter
methodology.
We constructed our steering filters to follow the sinusoidal pattern of the
model and changed our fitting goal to:
![]()
where ![]() is our steering filter matrix. As the right panel of
Figure toldi-steer shows we did a substantially better job
following ``geology'', with the added benefit of better vertically
constraining the interval slowness perturbations.
is our steering filter matrix. As the right panel of
Figure toldi-steer shows we did a substantially better job
following ``geology'', with the added benefit of better vertically
constraining the interval slowness perturbations.