




Next: CONCLUSIONS
Up: Bednar: Least squares dip
Previous: APPLICATION
Many enhancements to the process described above can be contemplated.
As suggested by Fomel 1997, one possibility is the extension of
Claerbout's (1994) least squares coherency
| ![\begin{displaymath}
coh_x = \frac{<\frac{\partial [u]}{\partial x}\times\frac{\p...
...tial [u]}{\partial t}\times\frac{\partial [u]}{\partial t}\gt}}\end{displaymath}](img9.gif) |
(6) |
to 3-D. In 2-D, this measure quantifies the quality of the planar fit and is
more statistically related to coherency than the dip-magnitude of Equation 5.
Clearly, direct comparison of the two methods suggest that coherency
will at least be better normalized. Figure 5 is a time slice at 2.76 seconds
after calculation of
| 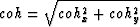 |
(7) |
for each point in the volume displayed in Figure 1. In the view of the
author this display is a much improved version of Figure 3. Moreover, the
volume display in Figure 6 indicates some improvement in the quality of
vertical sections as well.
Only a careful comparison of each volume in a valid interpretation setting will
reveal which result is more useful. Because it is better normalized,
coh should be easier to display and interpret than ||p||.
In addition to the two approaches described here, other ideas may prove
interesting. Estimates of local dip can be used to orient calculation of
other desirable statistical quantities. Given sufficient daring, one
can consider the computation of local curvature throughout the entire volume.
Displaying such values on a horizon slice through the volume
should provide estimates
of the local roughness and perhaps form a basis for fractal based prediction of
faulting below seismic resolution.





Next: CONCLUSIONS
Up: Bednar: Least squares dip
Previous: APPLICATION
Stanford Exploration Project
10/10/1997
![\begin{displaymath}
coh_x = \frac{<\frac{\partial [u]}{\partial x}\times\frac{\p...
...tial [u]}{\partial t}\times\frac{\partial [u]}{\partial t}\gt}}\end{displaymath}](img9.gif)
![\begin{displaymath}
coh_x = \frac{<\frac{\partial [u]}{\partial x}\times\frac{\p...
...tial [u]}{\partial t}\times\frac{\partial [u]}{\partial t}\gt}}\end{displaymath}](img9.gif)