




Next: APPLICATION
Up: Bednar: Least squares dip
Previous: INTRODUCTION
In his book,
Claerbout 1994 shows that filters
of the form
| 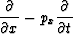 |
(1) |
destroy plane waves u(x,t) = u(t + px x). Letting 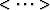 denote averaging
over time and
denote averaging
over time and ![$[\cdots]$](img3.gif) over space, the value,
over space, the value,
| ![\begin{displaymath}
p_x = \frac{<\frac{\partial [u]}{\partial x}\times\frac{\par...
...rtial [u]}{\partial t}\times\frac{\partial [u]}{\partial t}\gt}\end{displaymath}](img4.gif) |
(2) |
represents a smoothed least squares estimate of local dip. In the 3-D setting
one can calculate both, px, and,
| ![\begin{displaymath}
p_y = \frac{<\frac{\partial [u]}{\partial y}\times\frac{\par...
...rtial [u]}{\partial t}\times\frac{\partial [u]}{\partial t}\gt}\end{displaymath}](img5.gif) |
(3) |
to obtain estimates in the line and cross-line directions so that the vector
defines a local plane at each point in the 3-D volume. Its magnitude,
| 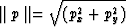 |
(5) |
is a scalar which responds in a somewhat dramatic fashion to relatively minor
deviations from local plane wave assumptions. The reasons for this response
may not be completely clear. For time-migrated 3-D volumes, 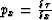 and
and
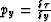 are estimates of the post-migration dip. For a given velocity,
they provide the basis for computing the zero offset point from which the local primary-reflection horizon
migrated. In this case, the dip-magnitude is in some sense porportional to the distance to this zero-offset location.
For large dipping events, such as faults, this distance can be quite large.
are estimates of the post-migration dip. For a given velocity,
they provide the basis for computing the zero offset point from which the local primary-reflection horizon
migrated. In this case, the dip-magnitude is in some sense porportional to the distance to this zero-offset location.
For large dipping events, such as faults, this distance can be quite large.
Abrupt changes in amplitude or wavelet phase can also result in major changes in dip-magnitude.
The quantities px and py are estimates of differential change and so will be significant whenever
discontinuities are present in the data volume.





Next: APPLICATION
Up: Bednar: Least squares dip
Previous: INTRODUCTION
Stanford Exploration Project
10/10/1997
![\begin{displaymath}
p_y = \frac{<\frac{\partial [u]}{\partial y}\times\frac{\par...
...rtial [u]}{\partial t}\times\frac{\partial [u]}{\partial t}\gt}\end{displaymath}](img5.gif)