Next: Nonhyperbolic events suppression
Up: Sun: Inverse NMO Stack
Previous: Inverse NMO stack operator
Like many other geophysical operators, the inverse NMO stack operator can be
coded in either ``push'' or ``pull'' forms, namely, we can loop over the
output space and ``pull'' a corresponding value from the input space, or loop
over the input space and ``push'' the value to an appropriate location in the
output space. The adjoint of a pull operator is a push operator and vice
versa, which I call implementation adjoint.
On the other hand, there is another scheme of implementing the geophysical
forward and adjoint operation, which seems to be more reasonable.
That is, using ``push'' in both the forward and adjoint operations. The
reason I say it seems to be more reasonable is because it is a kind of
energy-conserved scheme. For example, starting with a forward ``push''
operation, we
push all the input energy into the output space, then we push the energy back
into the input space by applying a adjoint ``push'' operation. Seemingly,
there is no energy loss during the forward & adjoint operation, and we should
be able to get the exact original input. Actually, since all the
implementations are discrete schemes, some kind of interpolation is
inevitable. The discrete adjoint ``push'' operation is not exact
adjoint as it should be in the continuous space. Therefore, the output of
adjoint operation will not be the same as the input.
I implement the inverse NMO stack operator using two interpolation methods,
nearest-neighborhood interpolation and linear interpolation.
If I implement the forward operation by ``push'' and the adjoint operation
by ``pull'', or vice versa, the results are correct and independent of the
interpolation scheme and the velocity type, as shown in Figure
1. In other words, if the geophysical forward and adjoint
operation loop over the same space (model or data), the result will be
acceptable.
dependent
Figure 1 Start with a stack trace in the model space (trace 0) and generate a CMP gather using the forward operator. Then calculate the best stack trace from the CMP gather (trace 2 to 6, from one to five iterations). Zero trace 1 and 7 represent the separations between the input, output, and difference. The difference (trace 8) is produced by subtracting the final output (trace 6) from the input (trace 0). Velocity is constant. (a) forward is ``push'', adjoint ``pull'', and linear interpolation. (b) forward is ``pull'', adjoint ``push'', and linear interpolation. (c) forward is ``push'', adjoint ``pull'', and nearest-neighborhood interpolation. (d) forward is ``pull'', adjoint ``push'', nearest-neighborhood interpolation. All the four results are accurate, which means the inverse NMO stack is numerically invertible in these specific implementation schemes.





Then I try to implement both the forward and adjoint operations
using ``push'' or ``pull''. As shown in Figure 2,
the results are unsatisfactory, no matter what interpolation and velocity
I use.
It means that, if the forward and adjoint operation loop over different
spaces, we cannot recover the original input.
independent
Figure 2 Same as Figure 1. (a) forward is ``push'', adjoint ``push'', and linear interpolation. (b) forward is ``pull'', adjoint ``pull'', and linear interpolation. (c) forward is ``push'', adjoint ``push'', and nearest-neighborhood interpolation. (d) forward is ``pull'', adjoint ``pull'', nearest-neighborhood interpolation. It is interesting to notice that the result of double ``push'' is always smaller than the original input and the result of double ``pull'' is always larger than the original input. The difference between the final output and input decreases with time. Because in the deep zone, the effect of interpolation is less than that in the shallow zone.





In seismic processing, we start with a CMP gather in the data space and want
to find the best-fit stack trace in the model space. Therefore, we only need
to think about the adjoint operation. In this case, I claim that the ``pull''
implementation is the only choice and the ``push'' implementation will give
an incorrect result.
Because in equation (1), we assume the RMS velocity is the
zero-offset velocity. The ``push'' scheme actually uses the RMS
velocity v(t) instead of 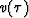 .
.
Figure 3 shows a CMP gather and its estimated depth-variable
RMS velocity. Starting with this CMP gather, I try both the ``pull'' and
``push'' scheme to invert for the stack trace.
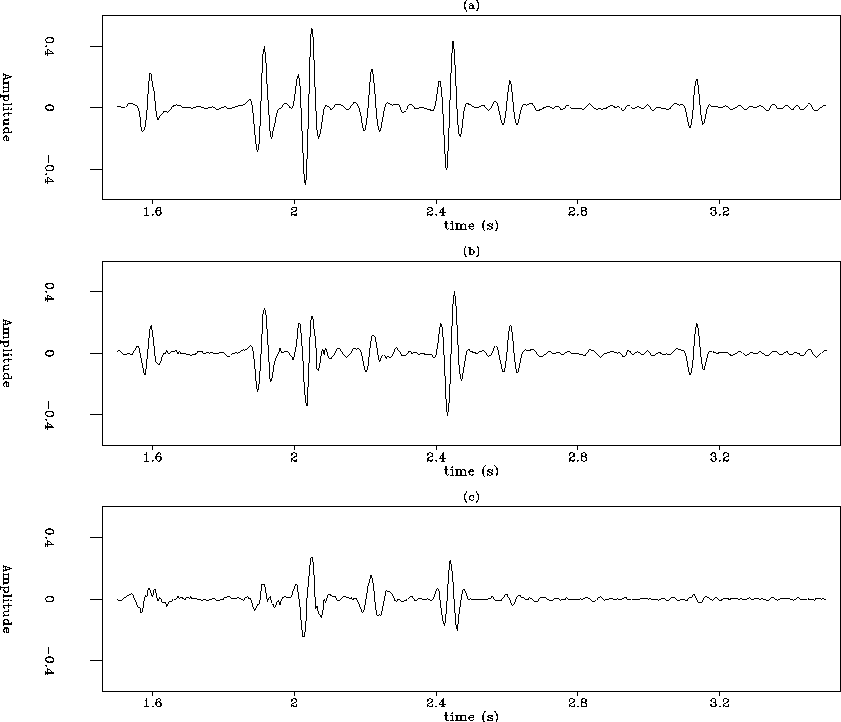
Figure 4 shows the results from the two schemes and also the
difference between the two schemes. The amplitude of the ``pull'' scheme
result is higher than that of the ``push'' scheme result. This means the
kinematic relation is better observed in the ``pull'' scheme. It is also very
clear that the difference becomes small in the deep zone. This is due to the
fact that the hyperbolic event becomes flatter with increasing time,
which makes v(t) similar to 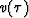 .
.
hp-input
Figure 3 (a) A synthetic CMP gather and (b) its estimated RMS velocity.




 hp-space
hp-space
Figure 4 Start with a CMP gather and end up with a stack trace. (a) the ``pull'' scheme result, (b) the ``push'' scheme result, and (c) the significant difference.





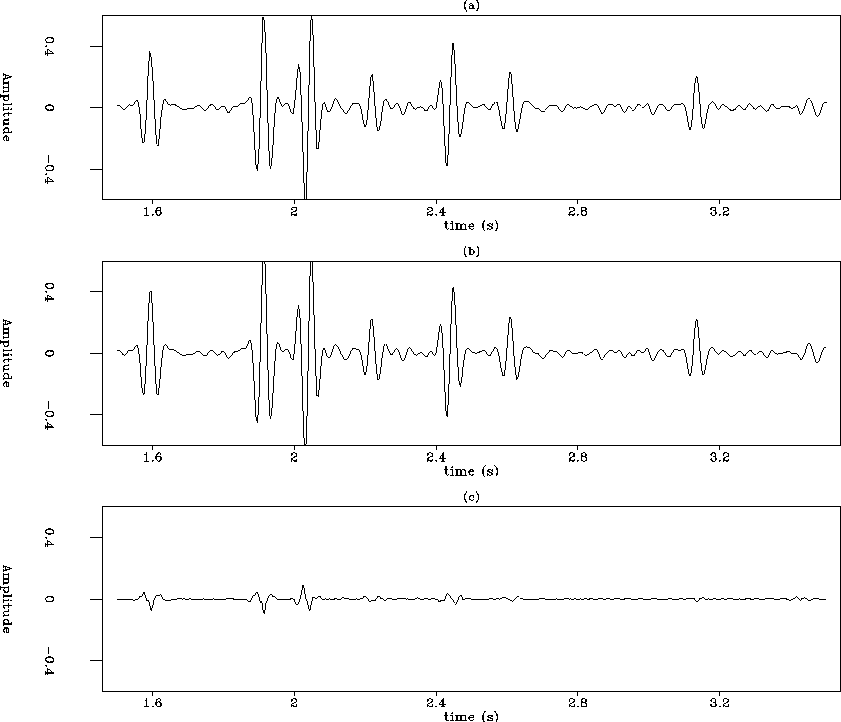
In order to verify the above conclusion, I compare the ``pull'' scheme result
with the conventional NMO+stack result (Figure 5). The
difference between these two approaches is negligible.
This proves that the inverse NMO stack is equivalent to NMO + stacking.
hp-stack
Figure 5 Same as Figure 4. (a) the ``pull'' scheme result, (b) the NMO+stack result, and (c) the minor difference.










Next: Nonhyperbolic events suppression
Up: Sun: Inverse NMO Stack
Previous: Inverse NMO stack operator
Stanford Exploration Project
11/11/1997