Next: About this document ...
Up: Alkhalifah: Prestack time migration
Previous: VTI homogeneous media
Although previous approximations of ph for horizontal reflectors in VTI media (Appendix B) yield
adequate results, better approximations based on
perturbation theory can further enhance the accuracy of the migration.
The theory is based on expressing the solution in terms of power-series expansions
of parameters that are expected to be small. As a result, higher power terms have
smaller contributions, and
as a result, they are usually dropped. The degree of truncation depends on the convergence
behavior of the series.
I will apply
the perturbation theory to evaluate the stationary-phase solution at px=0 and px=ph in
VTI media.
In the case of px=0, the stationary point solution ph, as we saw earlier, satisfies
| ![\begin{displaymath}
8 \eta^3 X^2 (1+2 \eta) y^4 - 4 \eta^2 X^2 (3+8 \eta) y^3 + ...
...X^2 (1+4 \eta) y^2 -
[X^2 (1+8 \eta)+ \tau^2 v^2] y + X^2 = 0, \end{displaymath}](img100.gif) |
(42) |
where y=ph2 v2. Analytical solutions for this quartic equation in y exist. They are, however,
complicated, and some of them actually do not exist ( ) for
) for  =0.
Recognizing that both
=0.
Recognizing that both  and ph can be small,
we can drop terms beyond the quadratic, as done in Appendix B, and solve the resultant quadratic equation
analytically. We can also benefit from fact that
and ph can be small,
we can drop terms beyond the quadratic, as done in Appendix B, and solve the resultant quadratic equation
analytically. We can also benefit from fact that  can be small and use perturbation series, that
is, apply a power-series expansion in terms of
can be small and use perturbation series, that
is, apply a power-series expansion in terms of  . Unlike
weak anisotropy approximations, the resultant solution
yields good results even for strong anisotropy (
. Unlike
weak anisotropy approximations, the resultant solution
yields good results even for strong anisotropy (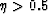 ). The
key here is to recognize the behavior of the series for large powers
of
). The
key here is to recognize the behavior of the series for large powers
of  using Shanks transforms. According to the perturbation
theory (Bender and Orszag, 1978), the solution of equation (C-1)
can be represented in a power-series expansion in terms of
using Shanks transforms. According to the perturbation
theory (Bender and Orszag, 1978), the solution of equation (C-1)
can be represented in a power-series expansion in terms of  as follows
as follows
| 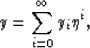 |
(43) |
where yi are coefficients of this power series.
For practical applications, the power series of equation (C-2) is truncated
to n terms as follows
| 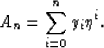 |
(44) |
The coefficients, yi, are determined by inserting the truncated form
of equation (C-2)
(three terms of the series are enough here)
into equation (C-1) and then solving for yi, recursively. Because  is
a variable, we can set the coefficients of each power of
is
a variable, we can set the coefficients of each power of  separately to equal zero.
This gives a sequence of equations for the yi expansion coefficients. For example, y0 is
obtained directly from setting
separately to equal zero.
This gives a sequence of equations for the yi expansion coefficients. For example, y0 is
obtained directly from setting  =0, and the result corresponds
to the solution for isotropic media.
For large
=0, and the result corresponds
to the solution for isotropic media.
For large  , An converges slowly to the exact solution, and, therefore, yields
sub-accurate results when used, even if we go up to
A10. Truncating after the second term (linear in
, An converges slowly to the exact solution, and, therefore, yields
sub-accurate results when used, even if we go up to
A10. Truncating after the second term (linear in  , A1) is
referred to as the weak anisotropy approximation. Using Shank transforms
(Bender and Orszag, 1978), one can
predict the behavior of the series for large n, and, therefore, eliminate the most pronounced
transient behavior of the series
(to eliminate the term that has the slowest decay). Following Shanks
transform, the solution is evaluated
using the following relation
, A1) is
referred to as the weak anisotropy approximation. Using Shank transforms
(Bender and Orszag, 1978), one can
predict the behavior of the series for large n, and, therefore, eliminate the most pronounced
transient behavior of the series
(to eliminate the term that has the slowest decay). Following Shanks
transform, the solution is evaluated
using the following relation
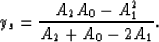
After some tedious algebra, done using primarily the Mathematica program,
ph corresponding to horizontal
events is given by
| 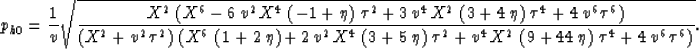 |
(45) |
Unlike equation (B-12), which corresponds to the solution of the quadratic
truncation of equation (C-1), equation (C-4) is valid for all practical models.
No validity conditions are required here.
The same steps used above to evaluate ph for px=0
is used for the case px=ph (ps=0), and, as a result,
| 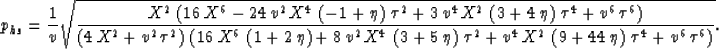 |
(46) |
Now, we insert the new definitions of ph0 and phs into equation (B-17):
| ![\begin{displaymath}
p_h = p_{h0} \frac{(1-2 \eta p_x^2 v^2)^4
(\frac{1-p_x^2 v^...
... \eta p_x^2 v^2-6 \eta (1+2 \eta) p_x^4 v^4]} [a(p_{h0})p_x+1],\end{displaymath}](img127.gif) |
(47) |
where
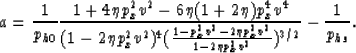
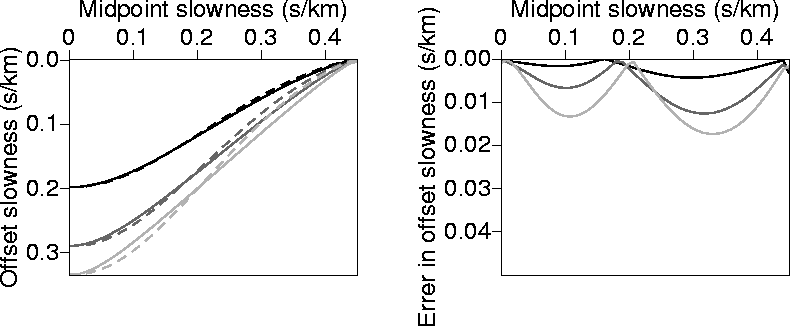
Figure C-1 shows a comparison between the exact ph solution of
equation (B-1) (obtained numerically)
and that given by equation (C-6) as a function of px for three sets of 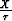 . The
absolute difference between the two solutions is also displayed. Clearly, results, obtained
using the modified equation, are far superior
to the ones obtained in Appendix B for VTI media.
. The
absolute difference between the two solutions is also displayed. Clearly, results, obtained
using the modified equation, are far superior
to the ones obtained in Appendix B for VTI media.
ph3sheta2m
Figure 23 Left: Values of ph as a function of px calculated numerically
(solid curves), and calculated analytically (dashed curves) using equation (C-6).
Right: The absolute difference
between the two curves on the left. The medium is homogeneous and isotropic with v=2.0 km/s.
The black curve corresponds to 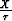 =1.0 km/s, the dark-gray curve corresponds to
=1.0 km/s, the dark-gray curve corresponds to
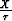 =2.0 km/s, and the light gray curve corresponds to
=2.0 km/s, and the light gray curve corresponds to 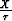 =3.0 km/s.
=3.0 km/s.






Next: About this document ...
Up: Alkhalifah: Prestack time migration
Previous: VTI homogeneous media
Stanford Exploration Project
11/11/1997
![]()
![\begin{displaymath}
p_h = p_{h0} \frac{(1-2 \eta p_x^2 v^2)^4
(\frac{1-p_x^2 v^...
... \eta p_x^2 v^2-6 \eta (1+2 \eta) p_x^4 v^4]} [a(p_{h0})p_x+1],\end{displaymath}](img127.gif)
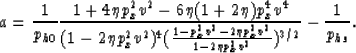
![]() . The
absolute difference between the two solutions is also displayed. Clearly, results, obtained
using the modified equation, are far superior
to the ones obtained in Appendix B for VTI media.
. The
absolute difference between the two solutions is also displayed. Clearly, results, obtained
using the modified equation, are far superior
to the ones obtained in Appendix B for VTI media.