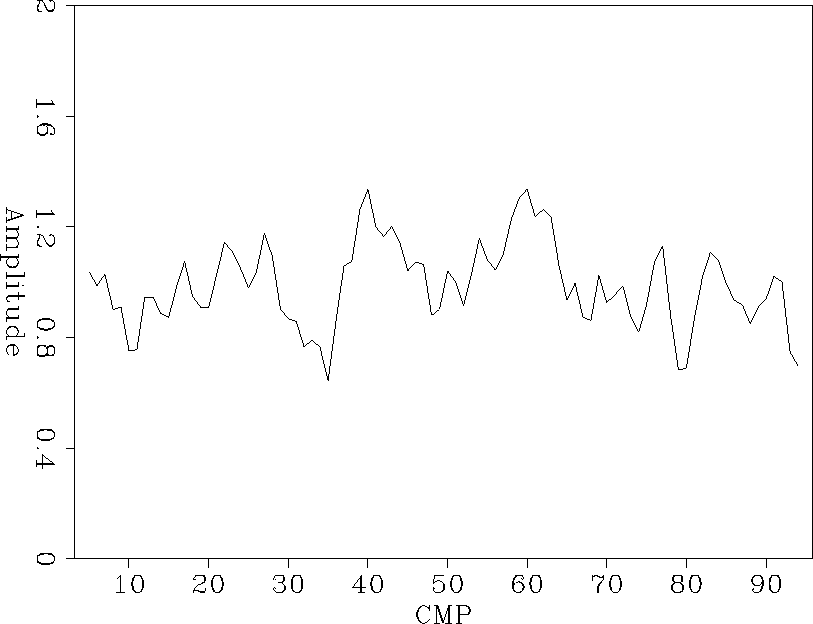Conclusions

We have presented a new technique to invert for reflectivity models while properly handling the irregular sampling of seismic data. The technique is based on the method of least squares and consists of a two-step solution for imaging. The data is equalized in a first stage with an inverse filter and an imaging operator is then applied to the preconditioned data to invert for a model. The equalization filter corrects the imaging operator for the interdependencies between data parameters. Each element of the filter is a mapping between two data elements. It reconstructs a data trace with given input geometry at the geometry of the other data element. The filter is therefore a symmetric AMO matrix with diagonal elements being the identity and the off-diagonal elements being the trace to trace AMO transforms. We tested the effectiveness of the method in the 2D case for the application of partial stacking by offset continuation. The equalization step followed by imaging has proved to correct and equalize the processing for the effects of fold variations by properly handling the amplitude and phase of the data.

 

input24
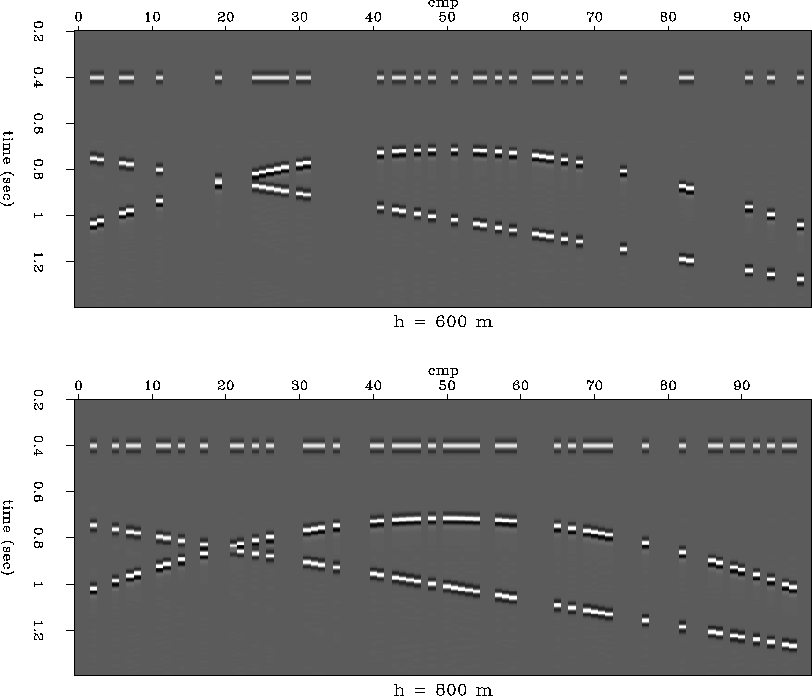
Figure 1 Irregularly sampled constant offset sections with 600 and 800m offsets.

 

input68
Figure 2 Irregularly sampled constant offset sections with 1000 and 1200m offsets

 

amo-600
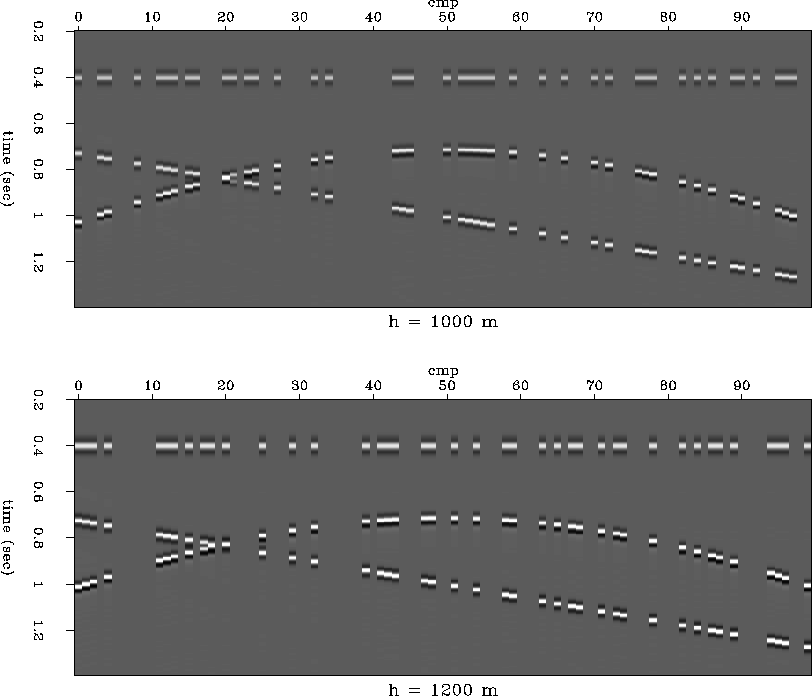
Figure 3 Offset continuation of irregularly sampled constant-offset section from 600m to 850m.

 

amo-1200
Figure 4 Offset continuation of irregularly sampled constant-offset section from 1200m to 850m.

 

fold
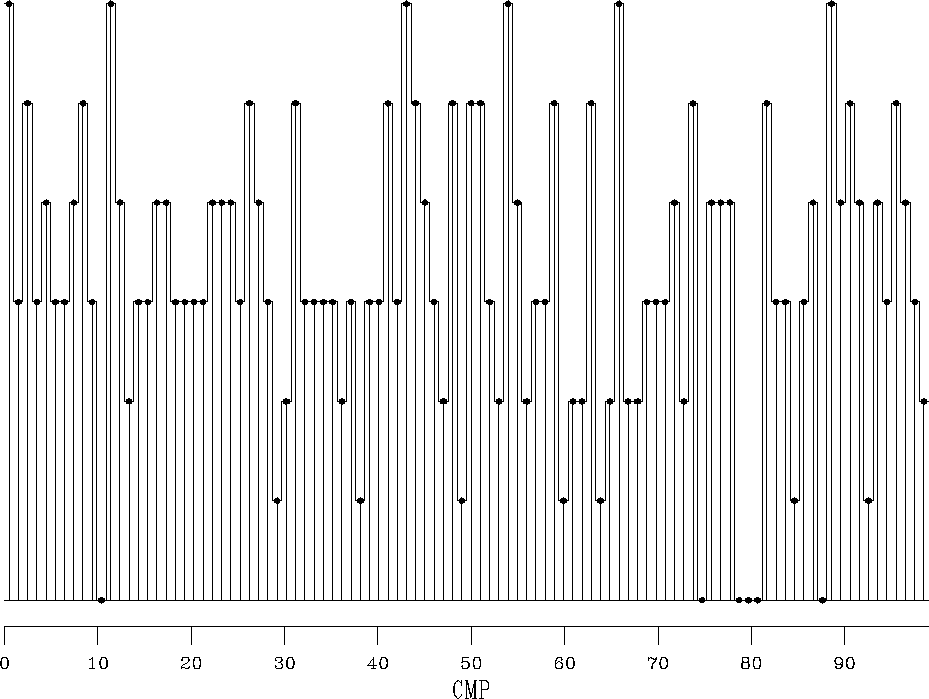
Figure 5 Fold distribution in the input data. The maximum fold is 7 and minimum is 0.

 

nmo-stack
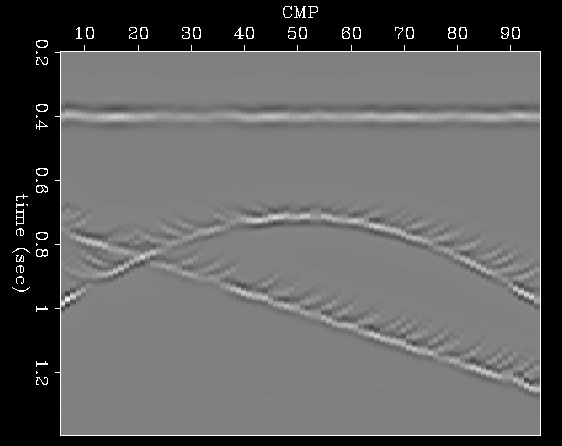
Figure 6 Partial stack after NMO and normalization by the CMP fold in each bin.

 

amo-stack
Figure 7 Partial stack after AMO to a common offset of 850m.

 

equal-stack
Figure 8 Output of the two-step inversion at an effective offset of 850 meters.

 

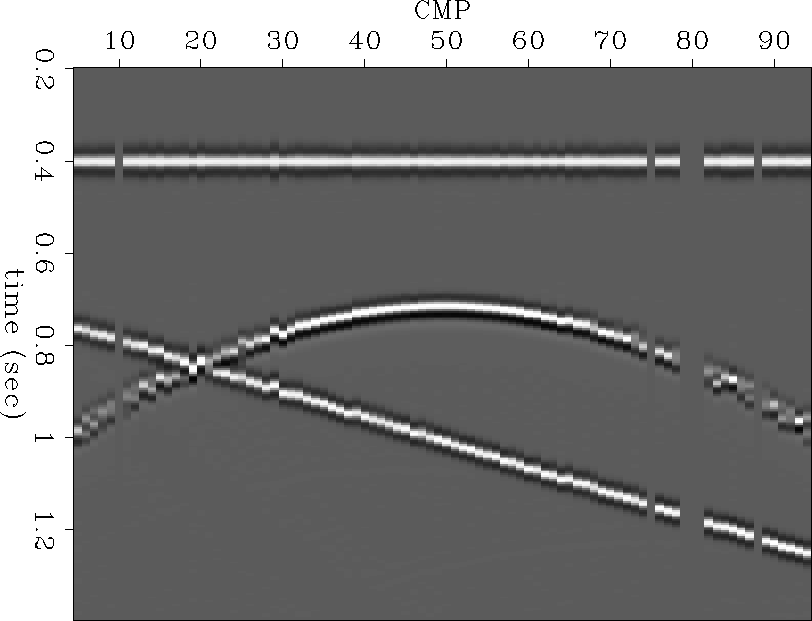
amo-stack-win
Figure 9 Window on the dipping events from the amo-stack result.

 

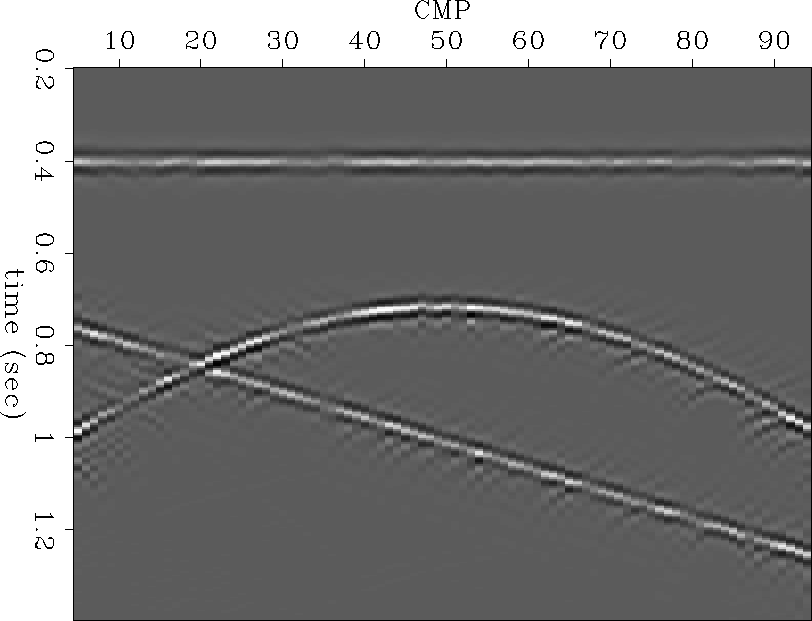
equal-stack-win
Figure 10 Window on the dipping events from the two-step inversion.

 

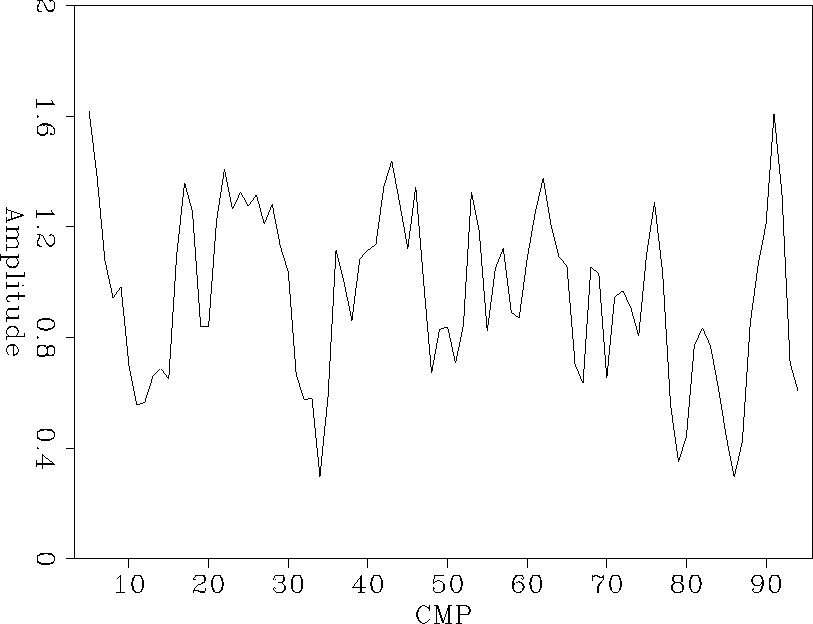
amp-amo
Figure 11 Peak amplitudes on the flat reflector from the amo-stack result.

 

amp-norm
Figure 12 Peak amplitudes on the flat reflector from the two-step solution.