Research Scenarios

To test Jag during its development, we implemented a small set of research scenarios:

• Deconvolution finds the wavelet for a given reflectivity and seismic trace
• Missing PE Filter finds the coefficients for a Prediction Error (PE) from given input data
• Missing Data (linear) reconstructs missing data in a two-step linear approach. First, the filter is found where the data is known. Once the filter is known, the missing data is found with the PE filter from the first step. This missing data problem involves compounding the convolution operator with a MaskingOperator that distinguishes the data locations where the data is known and where it is missing. We used two input data sets: a synthetic section and the Seabeam side-sweep sonar data from Jon Claerbout's book 1994.
• Missing Data (nonlinear) reconstructs missing data by a nonlinear approach. The filter and data are optimized simultaneously.
• Coherency with Patching computes a coherency attribute for a 3-D image volume. The process splits the image volume into subvolumes, finds a PE filter in each subvolume, filters the subvolume with the locally optimal PE filter, and finally merges the subvolumes back into a single image volume.
• TvDecon deconvolves a non-stationary time series. The process includes a leaking integration pre-processing step, and, since the problem is under-determined, a composition with the regularization operator, ${\bf I x \approx 0}$.

 

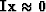decon
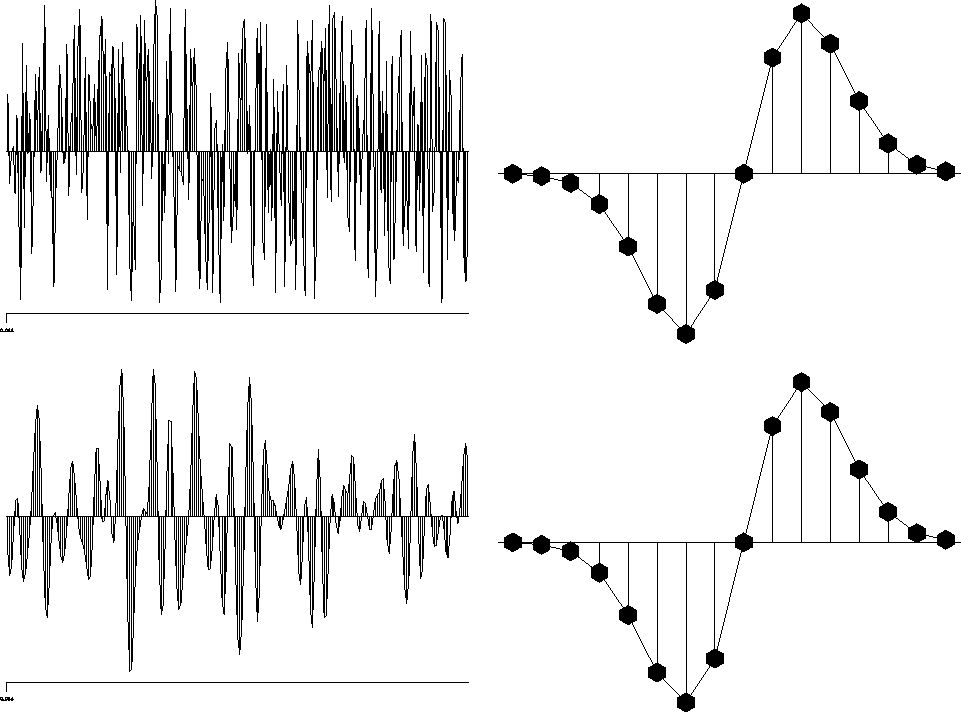
Figure 3 The signal at the upper left is a random reflectivity series. We compute the lower left signal by convolving the reflectivity series with a 16 point Ricker wavelet, which is shown in the upper right. We compute the lower right wavelet by inverting for an unknown 16 point wavelet given the two traces on the left. The CG solver finds the same zero-phase Ricker wavelet.

The code fragment progDecon is the main routine of the deconvolution problem. The class instantiates two Rsf. One contains a random time series, the other one the result of a convolution of the time series with a 16 point Ricker wavelet. Next the program instantiates an internal convolution operator. Since we are going to use a Conjugate Gradient solver, we create a positive-definite operator by recasting the operator and vectors according to the normal equations

$$\begin{eqnarray} {\bf A x} &=& {\bf b} \nonumber \\ {\bf A'A x} &=& {\bf A' b}. \nonumber \end{eqnarray}$$

Finally, we instantiate a CG solver, solve for the unknown wavelet, and write the wavelet to a file. Figure 3 shows the input and the result of the inversion.

 

/**
 * <BR><!-#include file="./source.inc"-><BR>
 */
/**
* I solve b = M x for x. 
* M is a    known convolution operator of the time series m (reflectiviy). 
* x is an unknown filter (wavelet). 
* b is a    known time series (seismic trace). 
* 
* I create the normal equations: b_L = M'b and L = M'M and 
* call a CGSolver to solve M'b = M'M x or b_L = L x. 
*/ 
public class IcafDecon { 
  public static void main(String[] args) {
    Rsf trace = new Rsf("./trace.H"); 
    Rsf rflct = new Rsf("./rflct.H");

hasAdjoint icaf        = new IcafFactory(rflct, trace.getSpace()); 
    Vector     traceNormal = icaf.adjoint().image(trace);
    CompoundLinearOperatorAdjoint
               icafNormal  = new CompoundLinOpAdj(icaf, icaf.adjoint());
    // Create an initial wavelet
    Rsf wave = (Rsf) icafNormal.getDomain().newMember();
    wave.zero(); 
    // Solve with CG solver and default solver settings
    new    CGSolver().solve(icafNormal, traceNormal, wave);
    // Write 
    wave.write(System.out); 
  }
}