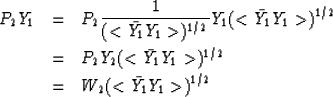Next: Implementation
Up: Schwab: 3-D Coherency
Previous: PREDICTION ERROR FILTERING
The central idea of pre-whitening is to use two PE filters. Each PE
filter minimizes the mean square energy of its output given its input.
However, the second filter is given the output of the first filter.
Once we have found the second filter, we apply it to the original input
(the input that we used to train the first filter). Obviously, the
second filter will not be optimal for removing the
predictable events of the original input.
As a matter of fact, the second filter is blind
with regard to the events the first filter removed from the data.
The second filter applied
to the original input will remove the components it was trained to
remove, but it will preserve the components that the first filter is
capable of removing.
Imagine that an input time series contains three predictable
components.
Given an input time series and a given filter length,
we find the first optimal PE filter. The data component this
first filter removes is the first predictable component.
If the spectrum of the input time series is Y1,
then a PE filter P1 corresponds to
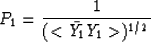
where 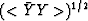 represents a smooth
version of Y's spectrum.
The output spectrum after such a PE filter step is
where W1 represents a spectrum that tends to be white.
If P1 were a perfect PE filter, then W1 would be
white. But since our PE filter implementations are
limited to a few coefficients, W1 only tends to be white.
represents a smooth
version of Y's spectrum.
The output spectrum after such a PE filter step is
where W1 represents a spectrum that tends to be white.
If P1 were a perfect PE filter, then W1 would be
white. But since our PE filter implementations are
limited to a few coefficients, W1 only tends to be white.
I define Y2 oas the utput of the first PE filter
| 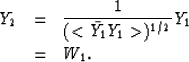 |
|
| (1) |
Consequently, the corresponding PE filter is
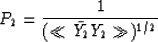
where 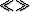 represents a smoothing
that might be different from the P1 smoothing <>.
Applying P2 to Y2 yields
where W2 represents a spectrum that again only tends to be white.
Substitution of the the expression 1 for Y2
yields
represents a smoothing
that might be different from the P1 smoothing <>.
Applying P2 to Y2 yields
where W2 represents a spectrum that again only tends to be white.
Substitution of the the expression 1 for Y2
yields
W2 = P2 Y2 = P2 W1
which indicates that W2 is whiter than W1.
If we apply the second PE filter, P2 to the original data spectrum Y1,
we finally get
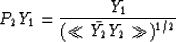
The simple identity
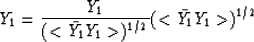
allows us to introduce Y2 according to expression 1
Consequently,
the resulting spectrum of the two step filter operation
is the product of the first predictable spectral component
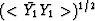 and the rather white spectrum W2. The second
predictable component
and the rather white spectrum W2. The second
predictable component 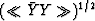 is removed.
In that sense
the cascading of PE filters implements a high resolution,
data adaptive notch filter. The component removed, however, is not
a fixed frequency component but a data dependent
band of predictable components.
is removed.
In that sense
the cascading of PE filters implements a high resolution,
data adaptive notch filter. The component removed, however, is not
a fixed frequency component but a data dependent
band of predictable components.





Next: Implementation
Up: Schwab: 3-D Coherency
Previous: PREDICTION ERROR FILTERING
Stanford Exploration Project
11/11/1997
![]()
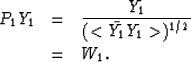
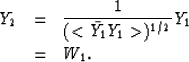
![]()
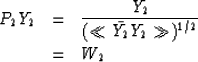
![]()
![]()