




Next: HINTS
Up: Claerbout: Diagonal weighting: An
Previous: INTRODUCTION
A reflectivity model 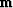 in geophysics
is a function defined in a physical volume
sampled densely enough to fill a computer's random access memory.
The volume typically has
somewhat fewer than about (103)3 = 109 elements (voxels).
The data
in geophysics
is a function defined in a physical volume
sampled densely enough to fill a computer's random access memory.
The volume typically has
somewhat fewer than about (103)3 = 109 elements (voxels).
The data 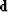 upon which the model is built
is a hundred to a thousand times larger, say 1011 elements
and generally requires many magnetic tapes.
Thus the matrix
upon which the model is built
is a hundred to a thousand times larger, say 1011 elements
and generally requires many magnetic tapes.
Thus the matrix 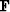 relating the data to the model would
have 1020 elements (which is a futile way to think about the problem).
What we can readily do is manufacture synthetic data from any model
by running a program that amounts to a matrix multiply
relating the data to the model would
have 1020 elements (which is a futile way to think about the problem).
What we can readily do is manufacture synthetic data from any model
by running a program that amounts to a matrix multiply
| 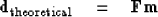 |
(1) |
By paying attention to some details
it is straight-forward
(in all the problems that I have encountered)
to write another program
that applies the transpose 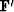 operator
to the data
operator
to the data 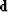 giving us a first guess at the model.
This first guess is called an image
giving us a first guess at the model.
This first guess is called an image 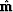 of the model
of the model 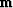 .
.
| 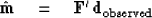 |
(2) |
The method of least squares offers the standard solution
| 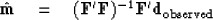 |
(3) |
which is wholly impractical because of the size of 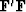 .This suggests we seek a diagonal matrix,
say
.This suggests we seek a diagonal matrix,
say 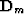 as an approximation for
as an approximation for 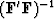 .
.
| 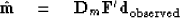 |
(4) |
At my request, Bill Symes offered a suggestion for 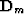 .His suggestion uses the
.His suggestion uses the 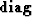 operator of matrix algebra
which simply takes a vector and distributes its components along
the diagonal of a matrix:
operator of matrix algebra
which simply takes a vector and distributes its components along
the diagonal of a matrix:
| 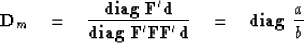 |
(5) |
This suggestion seems reasonable because the denominator
has two more powers of 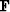 than does the numerator
and the suggestion seems wise
because it uses the known data
than does the numerator
and the suggestion seems wise
because it uses the known data 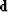 .Unfortunately, the denominator b can easily vanish.
To prevent such trouble we rearrange and smooth
.Unfortunately, the denominator b can easily vanish.
To prevent such trouble we rearrange and smooth
| 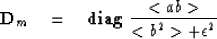 |
(6) |
where  is a positive number for experimentation
and the numerator and denominator can be locally averaged
as indicated by the ``
is a positive number for experimentation
and the numerator and denominator can be locally averaged
as indicated by the ``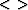 ''.
(Remember that the vectors
''.
(Remember that the vectors 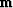 and
and 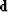 are
sampled representations of continuous functions of space and time.)
Our experience with Symes' suggestion
was disappointing, probably for the reason suggested next.
are
sampled representations of continuous functions of space and time.)
Our experience with Symes' suggestion
was disappointing, probably for the reason suggested next.
Besides the standard pseudo inverse
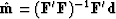 there is another
there is another
| 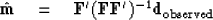 |
(7) |
that arises when a fitting problem is underdetermined.
This pseudoinverse
solves the problem of minimizing 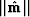 subject to the constraint equations
subject to the constraint equations 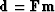 .This pseudoinverse suggests a right side diagonal approximation
.This pseudoinverse suggests a right side diagonal approximation
| 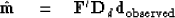 |
(8) |
I don't expect this
right-side
diagonal to work any better
than did the earlier
left-side
diagonal.
Experience with special cases suggests we need both
the data-space diagonal and the model-space diagonal, namely
| 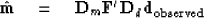 |
(9) |
Our challange for the mathematicians
is to give us some guesses for the diagonal matrices
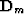 and
and 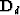 .This problem is one of
a very general nature,
far more general than the several applications
in which I have found it.
It is like the question, ``What is an all-purpose preconditioner?''
.This problem is one of
a very general nature,
far more general than the several applications
in which I have found it.
It is like the question, ``What is an all-purpose preconditioner?''





Next: HINTS
Up: Claerbout: Diagonal weighting: An
Previous: INTRODUCTION
Stanford Exploration Project
11/11/1997
![]() .His suggestion uses the
.His suggestion uses the ![]() operator of matrix algebra
which simply takes a vector and distributes its components along
the diagonal of a matrix:
operator of matrix algebra
which simply takes a vector and distributes its components along
the diagonal of a matrix:
![]() than does the numerator
and the suggestion seems wise
because it uses the known data
than does the numerator
and the suggestion seems wise
because it uses the known data ![]() .Unfortunately, the denominator b can easily vanish.
To prevent such trouble we rearrange and smooth
.Unfortunately, the denominator b can easily vanish.
To prevent such trouble we rearrange and smooth
![]() there is another
there is another
![]() and
and ![]() .This problem is one of
a very general nature,
far more general than the several applications
in which I have found it.
It is like the question, ``What is an all-purpose preconditioner?''
.This problem is one of
a very general nature,
far more general than the several applications
in which I have found it.
It is like the question, ``What is an all-purpose preconditioner?''