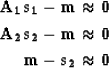
It is possible to construct many other operators which try to maximize the frequency content of the difference section.
For example another approach may be to find filters, A1 and A2, that when applied to unchanged areas of the two datacubes, s1 and s2, give the same result, m. In addition we wish the survey with the higher bandwidth to remain as unchanged as possible. These constraints are contained in the regression equations:
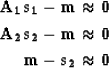 |
(8) | |
| (9) | ||
| (10) |
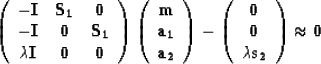 |
(11) |
Since we are estimating an intermediate model simultaneously with the
pair of filters, a good initial model speeds convergence. The initial
models chosen were ![]() and
and ![]() .
.
With two sets of regression, a good choice of ![]() is
important. A choice of
is
important. A choice of ![]() that is too large results in
that is too large results in
![]() and does not do a good job of match-filtering.
Alternatively, a choice of
and does not do a good job of match-filtering.
Alternatively, a choice of ![]() that is
too small does a good job of match-filtering, but a lot of the
resolution is lost and the result approaches that of the simple
inverse filtering above.
Unfortunately an intermediate choice of
that is
too small does a good job of match-filtering, but a lot of the
resolution is lost and the result approaches that of the simple
inverse filtering above.
Unfortunately an intermediate choice of ![]() is the worst of
both worlds, as it does a poor job of match-filtering and the
bandwidth of the signals are reduced. The results of the inversion
with
is the worst of
both worlds, as it does a poor job of match-filtering and the
bandwidth of the signals are reduced. The results of the inversion
with ![]() are shown in Figures 8. By playing
around with different values of
are shown in Figures 8. By playing
around with different values of ![]() and different filter
lengths, I was not able to get a successful result.
and different filter
lengths, I was not able to get a successful result.
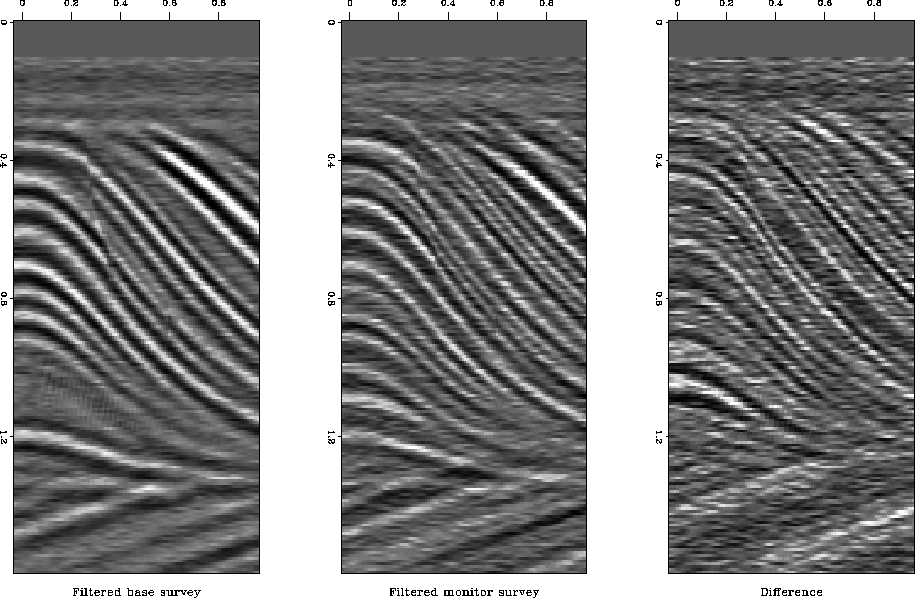 |
Although this approach looks like it may be successful on paper, I believe its failure stems from the size of the model space. Although time domain match-filtering uses a similar least squares formulation, it has only about a dozen elements in the model space, as opposed to a model the size of the data space which has to be estimated in this intermediate model approach.