Next: Results
Up: Malcotti and Biondi: Depth
Previous: Building and interpreting the
Depth focusing analysis is a methodology for velocity estimation based
on the fact that the total wave propagation time is invariant: the
total traveltime from the real reflection point obtained with the
real propagation velocity is equivalent to the total traveltime
obtained from the focus reflection image obtained with a wrong
propagation migration velocity plus a residual time related with the
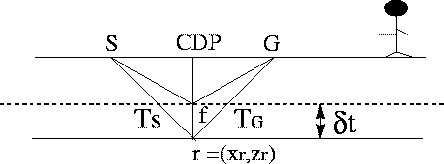
error in velocity. This residual time, in a horizontal stratified
media case with constant velocity Vr (see Figure 2), is equal to
a vertical time 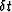 associated with a depth error
associated with a depth error 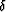 a paraxial approximation MacKay and Abma (1992):
a paraxial approximation MacKay and Abma (1992):
| 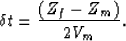 |
(6) |
homo
Figure 2 The residual time obtained when the
data is migrated with a migration velocity, Vm, greater than
the real propagation velocity Vr.

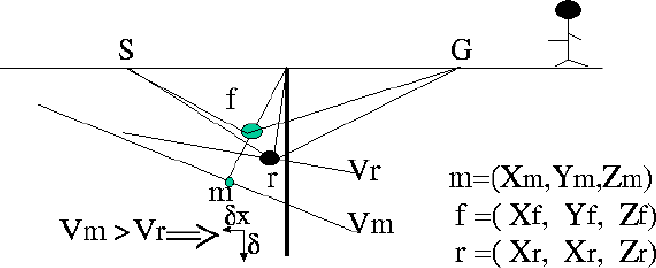
Figure 3 presents the migration of a dipping reflector with the media
velocity and with a wrong velocity Vm. Keeping the notation for
the migration velocity Vm, real velocity Vr, and the
downward continued point with the migration velocity to the imaging
condition m=(xm,ym,Zm), the real position of the dipping
reflector point is r=(xr,yr,zr) and the focusing point
is f=(xf,yf,Zf). The total time tT can be related
to the focus time tf by the following equation
MacKay and Abma (1992):
| 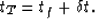 |
(7) |
This time equation in 2-D is rewritten using the offset, h, and the
dipping angle, 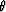 , in the law of cosines for the triangle obtained by
a image source (see Figure 3):
, in the law of cosines for the triangle obtained by
a image source (see Figure 3):
| 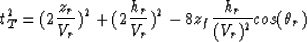 |
(8) |
| 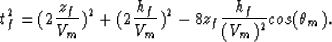 |
(9) |
Taking into account the previous formulas, we can conclude that in a subsurface
with dipping reflectors and lateral gradient velocity, the position of
the focusing point (xf,Zf) is not between the real position and
the migrated position, as it is in a lateral homogeneous media (i.e., constant
velocity media or horizontal layered media). Therefore, in
heterogeneous media the depth error panel needs to be corrected using
a residual zero-offset migration to move the depth error panel energy
to its correct position Audebert and Diet (1993). However, there is still error in
depth. Another way to understand this
mispositioning of the focusing point is to consider in the normal ray
as between the focusing imaging and CMP point at the surface. This
normal ray is different from the normal ray obtained with the real
velocity field, thus it has a different surface incident angle.
The focusing analysis methodology for 3D data is equivalent to 2-D methodology.
The depth error panel is built by extracting the zero offset trace from
every downward continuation step of prestack data recorded at the surface.
In this paper, the downward operator is a 3-D phase-shift in CMP domain operator.
It is important to point out, that in 3-D the focusing point has associated a depth error
and lateral position error in in-line and cross line directions. Therefore, to apply
equation (6) and (2), it is necessary to perform a
residual migration of depth error gather, then the
focusing point, the migrated point and the real point are along the same normal ray.
heter
Figure 3 The residual time
obtained when the data is migrated with a migration velocity,
Vm, greater than the real propagation velocity Vr.






Next: Results
Up: Malcotti and Biondi: Depth
Previous: Building and interpreting the
Stanford Exploration Project
11/11/1997
![]() associated with a depth error
associated with a depth error ![]() a paraxial approximation MacKay and Abma (1992):
a paraxial approximation MacKay and Abma (1992):