Next: Synthetic Example
Up: SCANNING HOMOTHETIC PARAMETER
Previous: SCANNING HOMOTHETIC PARAMETER
Audebert 1996 shows that if the slowness field is globally
scaled, ray geometry is unchanged.
Audebert 1996 points out that
starting from slowness field 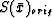 , the travel-time from
, the travel-time from
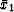 to
to 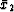 is:
is:
| 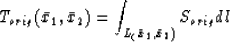 |
(1) |
where 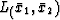 is the ray-path between
is the ray-path between 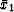 and
and
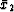 .
If we scale Sorig by a positive constant
.
If we scale Sorig by a positive constant 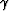 :
:
| 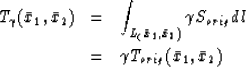 |
(2) |
| (3) |
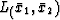 is the same in both cases because the original
Snell's law at each interface can
be reduced from the scaled travel-time version:
is the same in both cases because the original
Snell's law at each interface can
be reduced from the scaled travel-time version:
| 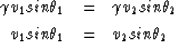 |
(4) |
| (5) |
As a result, scaled versions of the travel-time field represent valid
focusing operators. By finding the scaled (by 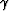 ) version of
the travel-time field that best focuses the data we get an estimate of
the error in our interval velocity model.
) version of
the travel-time field that best focuses the data we get an estimate of
the error in our interval velocity model.





Next: Synthetic Example
Up: SCANNING HOMOTHETIC PARAMETER
Previous: SCANNING HOMOTHETIC PARAMETER
Stanford Exploration Project
11/11/1997