




Next: 3-D dynamic ray tracing
Up: THEORY OF DYNAMIC RAY
Previous: THEORY OF DYNAMIC RAY
Assume that a ray is specified by the parametric equation
|  |
(2) |
where  is the traveltime along the ray, with
is the traveltime along the ray, with 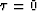 at the location of
the source. The independent variable is not necessarily
at the location of
the source. The independent variable is not necessarily  . It
can be any other variable which increases monotonously along the ray, e.g.,
arclength is a common choice in the ray tracing algorithm. Here we choose
traveltime because seismic data are sampled along time axis. Therefore, it
is more convenient to compare the ray tracing results with seismic data.
. It
can be any other variable which increases monotonously along the ray, e.g.,
arclength is a common choice in the ray tracing algorithm. Here we choose
traveltime because seismic data are sampled along time axis. Therefore, it
is more convenient to compare the ray tracing results with seismic data.
The three coordinates are the solution of geometric ray tracing system
| 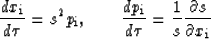 |
(3) |
where s is the slowness along the ray. The reason we use slowness, not
velocity, is to follow the convention of tomography. Here, 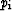 are the
Cartesian components of the slowness vector
are the
Cartesian components of the slowness vector 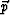 and
and
|  |
(4) |
Equation (3) is first-order ordinary differential
equations. Usually, we cannot find an analytical solution for a general
velocity model. It is more common to use some numerical algorithms, e.g., the
Runge-Kutta method. In this paper, we use a Fortran90 version Runge-Kutta
solver. In order to fit our expression to the
convention of rksuite90 package, the geometric ray tracing system is
expressed as
| ![\begin{displaymath}
\frac{d}{d \tau}
\left[\begin{array}
{cc}
x_1 & p_1 \\ x_2...
...\frac{1}{s} {\partial s \over \partial x_3} \end{array} \right]\end{displaymath}](img9.gif) |
(5) |
The initial condition is
| ![\begin{displaymath}
\left[\begin{array}
{cc}
x_1^0 & p_1^0 \\ x_2^0 & p_2^0 \\...
...n \beta_0 \\ x_{30} & s_0 \, \cos \alpha_0 \end{array} \right]\end{displaymath}](img10.gif) |
(6) |
where 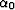 and
and 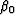 are the two initial take-off angles,
as shown in Figure 1.
are the two initial take-off angles,
as shown in Figure 1.
take-off
Figure 1 The initial condition of each central ray. (x, y, z) forms a Cartesian coordinate system. O is the source location.
|
|  |






Next: 3-D dynamic ray tracing
Up: THEORY OF DYNAMIC RAY
Previous: THEORY OF DYNAMIC RAY
Stanford Exploration Project
11/11/1997
![\begin{displaymath}
\frac{d}{d \tau}
\left[\begin{array}
{cc}
x_1 & p_1 \\ x_2...
...\frac{1}{s} {\partial s \over \partial x_3} \end{array} \right]\end{displaymath}](img9.gif)
![\begin{displaymath}
\left[\begin{array}
{cc}
x_1^0 & p_1^0 \\ x_2^0 & p_2^0 \\...
...n \beta_0 \\ x_{30} & s_0 \, \cos \alpha_0 \end{array} \right]\end{displaymath}](img10.gif)
![]() and
and ![]() are the two initial take-off angles,
as shown in Figure 1.
are the two initial take-off angles,
as shown in Figure 1.
